Computer Science AS
Introduction Information Representation Communications Communications 2 Hardware Logic Circuits Processor Fundamentals Assembly Language Monitor & Control System Software Security, Privacy & Data Integrity Ethics DatabasesAS Practical
Algorithm Data Structures and more Software developmentComputer Science A2
Data Representation File Organisation Advance Logic GatesInternet Virtual Machines System Software Encryption & Security Artificial IntelligenceA2 Practicals
Binary Search Linear Search Bubble Sort Insertion Sort Combined Algorithm Stacks Queues Linked List Binary TreeMore
Reference Pastpaper QuestionsGraphics, Sound, Two's Complement & Data Compression
Key terms
You will need to know some key terms before we get started:
1. Most Significant bit (MSB) - this is the bit in the binary number which is on the leftmost side of the bnary number and it carries the highest denary weight
2. Least Significant bit(LSB) - this is the bit on the rightmost side. It carries the lowest denary weight of one
3. Bit 0 is also considered as the LSB
Conversion
You will need to know how to convert from one number system to another:
1. Binary to Denary (vice versa)
2. Denary to Hex (vice versa)
3. Binary to Hex (vice versa)
We will talk about how each on is done briefly and I will also put a video for you to watch at the end of the chapter
Binary to Denary
Let's take a simple binary number
00110011
The binary value has a place value of 2x
The LSB has a weight of 1 and the 2nd bit has a weight of 2 and so on
So whenever there is a 1 you take that particular place value weight of that digit
Do the same for all other digits which are 1
Then take the sum of all the weights and it will give you the denary value
0 0 1 1 0 0 1 1
- - 32 16 - - 2 1
32+16+2+1 = 51
There is also another method you can follow
00110011
You start with the MSB
First mutliply the MSB with 2 then get the value
After you find the value you add either 1 or 0 depending on the next bit
Then the new value is multiplied by 2 again and the whole process continues
When you receive the last digit(LSB) you just add the bit to the value and this gives you the denary value
0 * 2 = 0 (add 0) 0 * 2 = 0 (add 1) 1 * 2 = 2 (add 1) 3 * 2 = 6 (add 0) 6 * 2 = 12 (add 0) 12* 2 = 24 (add 1) 25* 2 = 50 (Finally just add 1) 50 +1 = 51
This is my opinion a good method to follow
Denary to binary
There are also two methods for this
We will take the denary value 254 as the example
So we keep dividing the denary value by 2. We will sometimes get a remainder of 1 or 0. Then you read the remainders from the bottom to the top which gives us the binary number
2|254 2|127 → 0 2|63 → 1 2|31 → 1 2|15 → 1 2|7 → 1 2|3 → 1 2|1 → 1 0 → 1 Binary number = 111111102
We will also talk about the next method also
These requires you to know the binary weight properly such as 1 , 2 , 4 , 8 , 16 , 32....
This is very useful to convert a decimal number to a binary number (This is an A2 topic so we will discuss that later)
254 - 128 → 1
126 - 64 → 1
62 - 32 → 1
30 - 16 → 1
14 - 8 → 1
6 - 4 → 1
2 - 2 → 1
0 - 1 → 0 // as 0 is not large enough to reduct 1
from it
It is better to chose one method or else you would get confused
Binary to Hex
This is the easiest conversion
We group the binary numbers to nibbles starting from the right and we find the denary value of each nibble and this is converted to Hex ( very similar to BCD )
0011011
As we can see, this has 7 bits so how can we group in 4 bits
(0)001 1011
You need to add a 0 to the start to make it 4bits
0001 1011
1 11
1 B
= 1B16
To convert from Hex to binary follow the reverse order
1 B 1 11 0001 1011
Hex to denary (Vice versa)
There is a method to convert hex to denary and back directly but I won't recommend it to you
Its better to convert denary to binary then Hex ( vice versa ) as this is more simpler and less error prone
Prefixes
Same as physics, we don't like to give storage or other specifications in large numbers, we usually like to give it in 1 d.p
Here are the Decimal/denary prefixes
| Prefix | Magnitude | Symbol |
|---|---|---|
| kilo | 103 | KB |
| Mega | 106 | MB |
| Giga | 109 | GB |
| Tera | 1012 | TB |
This means that the size of data is grouped in quantities and the prefix tells us the size of data
However, recent questions don't ask this now but, lets see one example
Convert 200000 Bits to MB
First convert the bits to bytes
200000/8 = 25000Bytes
Then to convert to MB just divide by 106
25000/1000000 = 0.025MB
But now we use binary prefixes because it is the correct way of representing quantities
| Prefix | Magnitude | Symbol |
|---|---|---|
| Kibi | 210 | KiB |
| Mebi | 220 | MiB |
| Gibi | 230 | GiB |
| Tebi | 240 | TiB |
This is a bit complex and requires you to do a lot of workings
Lets take the same example
Convert 200000 Bits to MiB
Note now it MiB
200000/8 = 25000Bytes
25000/1024 = 24.4KiB
24.4/1024 = 0.024MiB
So really they will usually specify which one they want. If they say KB use denary prefixes. If they use KiB use binary prefixes
Also if they say Mib instead of MiB it means they want Mebibits not Mebibytes and so you don't have to divide by 8
Internal Coding Numbers
The computer follows two's complement when storing numbers
There are two types of integer which the computer can store - unsigned and signed integer
Signed integers are integers which can be either positive or negative whereas unsigned integer is always positive
Sign and Magnitude
This is the common form when we display signed integers
The Most significant bit determines the sign ( 1 - negative and 0 - positive ) where as the rest of the bits define the magnitude
For example 10110110
The Most significant bit is 1 and so this is a negative number
If we convert the rest of the bits to denary 54 which is the magnitude
So this byte represents -54 only if this byte is a signed integer
If it is not a signed integer we just use normal conversions like the above examples
So most questions give the byte in a sign and magnitude form ( unless they state the form ) and this must be converted to two's complement
They might ask like this
Convert this signed integer to 2's complement -
10011110
Before you know how to convert it we need to first define 2's complement
Two's Complement
This is one's complement plus 1
What is one's complement?
One's complement is when the bits in a byte are substracted from 1 ( so making a 1 to 0 and 0 to 1
An example is 00100100 is converted to 11011011 - so every bit is changed
To find two's complement we just need to add 1 to the 11011011
don't use this method as it is quite confusing
To convert a binary number to two's complement directly, follow this steps
Lets take an example
10011100
Ignore the first 0's on the right side
And also ignore the first 1 on the right
Then invert all other bits - convert 1 to 0 and 0 to 1
So we will get:
01100100
This is a much easier method and usually used to change negative sign and magnitude binary numbers
Here's the catch!
The computer follows 2's complement and so sign and magnitude numbers must be converted using the above method
However you use this method only when the sign and magnitude is negative, infact this is a very confusing part
If the binary number is positive then the sign and magnitude is the same as the two's complement form
Lets see an example:
Convert 01101111 to 2's complement
The answer is again 01101111 and we will see why later
Convert 10010010 to 2's complement
So for this we need to use the above method and so you will get 01101110
However this is not the answer because the first bit(MSB) is changed from 1 to 0 and so it will become a positive number
For this reason the Two's complement should have the same sign as the sign and magnitude form
The final answer must be 11101110
Why do they follow this
There is a reason why they follow this wierd method and it's because it makes converting from Two's complement to denary much quicker and direct
To convert a 2's complement to the corresponding denary value can be done by reversing the process such as finding the sign and magitude form and then finding the denary value
Or
There is another simpler method
The below binary value is in 2's complement. Find the denary value
11011010
The most significant bit is 1 so the number is negative
We know that the MSB carries the highest value of 128
The method follows like this:
First find the value of the sign which is negative and then add the positive value of the magnitude(remaining bits)
-128 + (64 + 16 + 8 +2 ) = -38
As the MSB is 1 then the value would obviously be negative
This is the easiest and fastest method
So this makes sense why the sign and magitude of positive number is the same as the two's complement
The below binary value is in 2's complement. Find the denary value
01011010
By following the same method above we will get 38
I don't know if textbooks follow this explanation but in my opinion this is the most simplest explanation I could give
Properties
There are some properties of 2's complement and sign and magnitude you need to know
Two's complement has only one representation for 0 where as sign and magnitude have two forms - one for -0 and one for 0. This is actually an advantage of two's complement
The maximum value which can be represented for signed integers using 4 bits is 2n-1 = 7
The largest negative number formed is -2n = -8
Binary aritmethics
Lets see an example
01011101
01111011+
________
11011000
To do this just follow the normal addition
Binary addition begins from the rightmost side
If 1 + 1 then it gives 0 and 1 is carried
If 1 + 0 then it gives 1 and no carry
If 1 + 1 + 1 then it give 1 and a carry of 1
If 1 + 1 + 1 + 1 then it gives 0 and a carry of 2
There is a pattern if you can see if the summed value is a multiple of 2 then we get 0 if not we get 1
The carry is the number of 2's which can fit the summed value
don't worry I will include a video for all these calculations below
There is also another longer method and that includes converting the binary number to denary and doing the calculation
Lets see an example now to substract binary numbers
01111101
01111011-
________
00000010
Binary substraction begins from the right side to the left side
If 1 - 0 then it would be 1
If 1 - 1 then it would be 0
If 0 - 1 then it gives 1 and borrows one from the next digit
Why does it becomes 1? Because when we borrow 1 we get 2
Overflow errors
It is when the result of a calculation is larger than the number of bits used to define the storage for the result
So sometimes when you add 2 binary number the result may have more number of bits
1111
1111+
_____
(1)1110
Sometimes these overflow can cause the result to become negative when we add two positive numbers
0111
0111+
_____
1110
Or when two negative numbers are added it can produce a positive number
10100000
10100000+
________
(1)01000000
The (1) will not be recorded as it won't fit in the storage, so then computer will read this as a positive number which is wrong
Both of these examples are overflow errors and the processor must be able to identify these - we will see them more in Assembly language chapter
BCD - Binary coded decimal
Denary digits are represented using nibbles or 4 bits
4 bits can be used to represent a single denary digit from 0 to 9
If the nibble contains a value of more than 9 then it is called an invalid BCD
There are 2 types of BCD - packed BCD or one BCD per byte
In packed BCD it means that 2 digits of denary can be represented using 1 byte, whereas in one BCD per byte only one digit is represented(the remaining bits are 0's)
Example, Packed BCD - 11011001 and One BCD per byte - 11010000
So how do you convert it to denary digits
For example 00100111 is a packed BCD
We can break it to two nibbles
0010 1001
Each nibble could be converted to the corresponding denary value
| 0010 | 1001 |
|---|---|
| 2 | 9 |
This gives a value of 29
If the nibble had a value of more than 9 then it is invalid
BCD is used to display denary digits in calculators and watches
You also need to know how to perform calculations and addition with BCD
When we do addition with BCD we isolate each nibble such as the example below
29 + 45
0010 1001 (29)
0100 0101 (45)
____ ____
0110 1110
0110
0110 (1)0100
0111 0100 (74)
So to correct this we need to always add 0110 or 6
We can see after adding 0110 we get a carry of 1 which taken to the next BCD and added
If the next BCD also was invalid then we had to add 0110 and 1 = 0111 and there will be a carry to the next BCD
Internal coding of character
There are two ways which text and characters can be represented
- ASCII
- Unicode
American standard code for information interchange
Originally ASCII uses 7 bits to store each character(this is known as the ANSI ASCII)
The bits required to store each ASCII character are known as character codes
This could be used to represent 128 different characters which is enough to represent the english set and numbers and other command keys
The new ASCII is called the Extended ASCII as it is used to represent modified alphabets such as the ISO - Latin characters
This uses 8 bits or 1 byte to store each character and this could represent 256 characters
This is still not enough to represent other characters from different languages
The standard uses 2 bytes to store each character allowing 65536 possible characters
However most of the time its usually less as some bits are required to describe the encoding used
UTF - 8 and UTF - 16 bits means that in UTF - 8 the system handles each 8 bits at a time.
Unicode use the term code point instead of character code
Unicode is able to represent all the characters in the world and many other language so it used more commonly than ASCII
Unicode code point are usually represented using Hexadecimals - for example U - FFFF
Notes in ASCII
All you need to know is ASCII is enough to represent the english character set and numbers and some commands
Characters which are in sequence are changed by the ASCII value of 1 - Ex A and B are only different by one value
The difference between the uppercase and lowercase ASCII characters is in bit 5 - Ex (A=65) where as (a=97) so difference in 32
Representation of graphics
There are 2 types of graphics:
- Vector Graphics
- Bitmap Graphics
- Lossless Compression
Graphics made out of drawing objects and their associated properties
So these drawing objects are shapes
A drawing object is component which is defined using geometric formulae
This follows a very simple idea, the image is made up of shapes or components which are defined using a drawing list
A drawing list is a list which contains one set values that contains many attributes for each drawing objects
So the drawing list contains a list of attributes which defines a property of the drawing object
A property is an aspect of the appearance of the drawing object
An example of the property includes the radius or the color or the border
Vector graphics are stored in the SVG format and requires a graphic plotter to output them directly
Vector graphics are relative to the canvas and so it is scalable without geting distorted and pixelated
Also when image is scaled both the dimensions are scaled so the image doesn't get squashed or stretched
Another important point is that vector graphics uses a lot of processing power however less storage compared to BMP graphics and it is also used to represent simple images such as shapes
If an vector graphics must be displayed on a screen or printed then it must be be converted to bitmap form
An image which is made out of elements or components called pixels which stores a color and its position in the BMP matrix
The pixels are displayed in a 2D matrix where the color of each pixel and its position in the 2D matrix is stored
Pixel is the smallest component which is identified using its color and position in the 2D matrix
So each pixel can represent a color and the number of bits required to store each pixel is known as color depth
Color depth is the number of bits required to store each pixel
The color depth of the pixel determines how many possible colors the pixel can represent
For example 24 bit color depth means that 224 colors can be represented
Some questions use the word bit depth for images and this means the number of bits required to store each primary color
For example if you have a bit depth of 8 bits it means it requires 8 bits to store each primary color of RGB and so the color depth will be 24 bits
Bit depth is the number of its required to store each primary color
So back to BMP images it is made of many tiny pixels in a 2D matrix. To find the number of pixels in a image we need to find the product of the pixel high and pixel wide of an image, this is known as the image resolution
Image resolution is the product of the number of pixels high and number of pixels wide an image is
In a simpler terms, it means how many pixels are there in an image
The same concept could be applied for display screen
The screen resolution is the product of the number of pixels high and number of pixels wide the screen can display
So whatever we see through the screen, it is limited by the screen resolutuion - for example if the screen is 2K but the image is 4K we will only see a 2K image
There are some points on Bitmap graphics - it uses the file extension .BMP(raw file) where as the compressed versions are .PNG and .JPG
Also the bitmap images can be enlargened but, when we enlarge the image even the pixels are enlarged and so the image seems pixelated and distorted
Bitmap images are good for storing photographs and pictures but uses way alot of storage
Image file size
They will ask us to calculate the file size of an image
We find the number of pixels(using the image resolution) and multiply it by the color depth
File size = Resolution * Color depth
Even bit depth could be used but we need to then multiply by 3
File size = Resolution * Bit depth * 3
Depending on what you took for the color depth ( if we took it in bits ) then the file size will be in bits
In my opinion it's better to use bytes as you may have to convert it to MiB
Let's take an example
What is the image size if the pixel height is 500 and the pixels wide 1000 and the color depth is 24 bits
File size = Resolution * Bit depth * 3
Resolution = Pixels high * pixels wide
File size = 500 * 1000 * 3
File size = 1500000 Bytes
To convert it to MiB we need to divide by 1024 and again by 1024
File header
The above calculated value gives the space required only to store the graphics however at the start of the file there is a file header which provides metadata of the file
Number of bits at the start of a image file which is used to define the coding used such as the color depth and the resolution
These are the things defined by the file header:
1. Image resolution
2. Color depth and the coding schemes
3. Image name and type
4. Compression techniques used(if any)
Sound Representation
Sound waves in the air are analogue waves which contain a range of values and amplitudes and must be converted to the digital forms, we will discuss each point in detail
Sampling
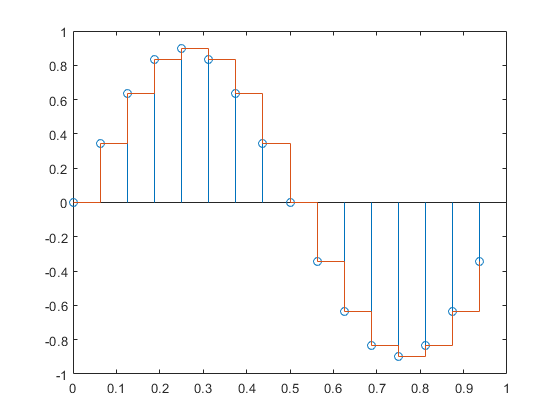
It is taking regular measurements of amplitudes at set timed intervals (regular intervals)
So for the ADC convertor to convert from analogue signals to digital it must take the amplitude at regular intervals and digitise them to binary.
Another point to remember that there is usually a band-limiting filter in the sound encoder(instrument for recording and digitising sound) to remove high frequency which can not be heard by the human ear
Sampling Rate
This is also known as sampling frequency
The number of samples recorded per second
This makes the sound more clearer/smooth and high quality as there is more changes in the sound per second
Sampling resolution
The number of bits required to store each sample
This is also known as bit depth
The definition is easy however the understanding is also required - greater bits required to store each samples means more possibilities of amplitude can be recorded, this means if 3 bits are used to store each sample, then the sample can represent 8 different sound levels or amplitudes
Usually 16 bits are required for good quality and to avoid any quantinising errors
Higher sampling resolution means the sound is more crisp
Sound file size
The method for calculating sound file size is also required
File size = Sampling resolution * Sampling frequency * Duration * channels
Again if we use bits for the sampling resolution we get the answer in bits
Duration must be in seconds
Compression Teachniques
Remember that there are two types of compressions:
This when no data is removed and the process could be reversed to obtain the original file - these include RLE and Huffman coding algorithms
Usually there are two algorithms used for lossless compression:
RLE - Run length encoding is done by specifying the number of times a character is repeated followed by the value of the character
For an example AAAAAAAA - 8A
RLE is not strictly marked as it is the concept which matters, usually RLE can be in Hex or Binary and the order of the representation doesn't really matter - so 8A is same as A8
Huffman coding - this replaces the most frequently used characters or words with shorter codes
Huffman is known by many other names such as indexing, dictionary
Usually we have a table which contains the character which is being replaced and their shorter codes
Huffman coding can be used for sound also to replace most frequent amplitudes with shorter codes
Lossy Compression
This method removes unnecessary data which the process can not be reversed to obtain the original file
This is done by reducing the image or sound quality by reducing the color depth or the sampling resolutions
Removing slight changes in shade of color in images with one color
Using perceptual shaping where frequency which are inaudible are either removed or stored with lower sampling resolutions
The resolution of the image can also be reduced
The problem is the quality is reduced but managable to the user
When defining each type of compression give an example for each
Recommended
These are things you might like. Clicking these ads can help us improve our free services in the future...
End of Chapter Videos
Collection of Videos to Support Your Understanding.
Remember these videos are handpicked by me and I feel these are one of the best ones out there. But I constantly update this list for each chapter.The Youtubers are more than welcome to contact me.
Also, don't forget to Subscribe to our Youtube channel - Wiscus
Watch
