Charges, Electric Fields & Field Strengths

This chapter discusses about stored charges instead of moving charges ( Electricity ).

Basics?

All charges produces an electric field around it like magnets!

You need to know the basic concepts in electric fields such as the basic definitions and ideas but, let's start with the most basic truth

Point charges

We see two positive charges below. They do not attract but, repel. This is the same for two negative charges

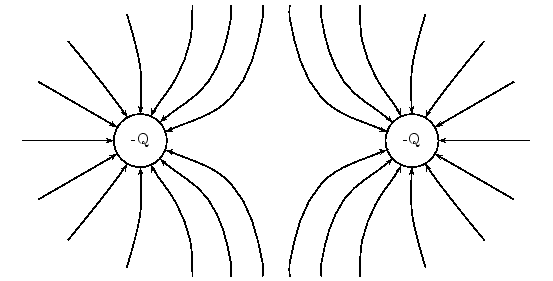
However, two unlike charges such as a positive and a negative charge wil attract each other

We need to know what are electric field lines of a point charges

Always the electric field goes from positive to negative

Point charges have a radial electric field

And so an isolated positive charge always has electric field lines going away from it. Whereas, a negative charge always have field lines directed towards the charge but, what is an electric field and these lines!

Electric field

A region in which a positive charge experiences a force

The definition is defined for a standard charge (+). Alse this region is not visible but, we represent them using electric field lines

You will need to know some basic principles of electric field lines

• The direction of electric field lines

The direction actually shows the direction of the force which a positive charge experiences ( as according to the definition ). So we actually place an imaginary positive charge to show the force it experiences at that particular point. This is because, most electric fields are not uniform!



For example below, we see that a positive charge q experiences a force F. So when we change the position of the charge it experiences a different force


• The spacing between the electric field lines show us the strength of the field

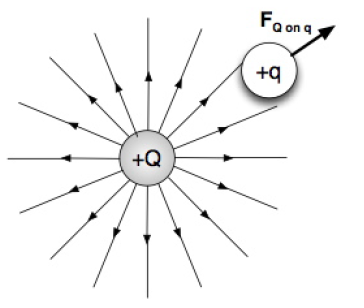
So actually when the lines are more closer, a greater force per charge is experienced compared to the same charge in a more spaced electric field lines

When the electric field is said to be uniform. The force remains the same at any point




Electric field Strength

It is the force acting on per unit positive charge

Again by definition, it's defined for a positive charge. This is very important as this shows that the direction of the electric field is in the same direction as the force experienced by a positive charge. This makes sense because, electric fields are from positive to negative. The positive charge always moves towards the negative plate.

E = F/q

The idea is very simple. If we want to find the electric field at a point, we find the force acting on that particular charge per unit charge

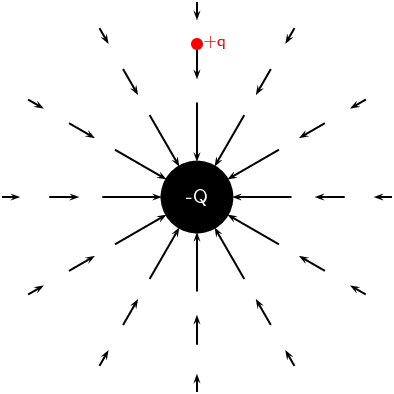
Say a charge Q has an electric field around it and another charge q is placed in that field. The charge q experiences a force F. So what is the electric field strength exerted by charge Q?

Now we need to understand that Electric field strength is the force acting on per unit specified charge. The force F per unit charge q gives the electric field strength of the Charge Q. This is very confusing but, actually it's simple.

Think of yourself and the earth. You have a weight or Gravitational force exerted on you and to find the gravitational field strength g. We just need to divide the gravitational force over mass.

g = gravitational force/m

However, we calculate gravitational force or weight using g again but, in A2 this is not the case and there is a different way of calculating gravitational force known as Newton's universal law of gravity. Likewise, Electrostatic force is calculated using Columb's law which will be covered in A2

So simply to find the electric field strength we need to divide the force/charge

Electric field = F/q

In this case, it's q and not Q. So this shows the electric field strength of Charge Q. Another way to see this is that in Columb's law we use both Q and q to calculate the force and dividing the force with q will cancel off q

F/q = KQq/q

F/q = KQ

This is not the equation but, a way to remember that by dividing by charge q we get the electric field strength of charge Q

Usually the electric field strength caused by a charge is not uniform so they may change from place to place. So the electrostatic force changes




If we want to find the electric field strength of the charge q we need to divide it by the charge Q

E = F/Q

Because according to Newton's 3rd law both experiences the same force. So this is very important.

To find the electric field strength of a Charge q due to a field created by charge Q. We need to find the force acting on q and divide by q

E = F/q



E - Vector?

Electric field strength is actually a vector just like g.

Actually when we define the direction of the electric field as positive, we use a positive charge. This literally means this particular charge experiences a force from positive to negative direction - which is in the same direction as the electric field

Eq = F

If the electric field strength was 2000NC^-1

What is the force experienced on an electron?

2000NC^-1 * -1.6*10^-19 = -3.2*10^-16N

So the force is negative and so this is realistic as Electric fields are always from + to - . The force is towards - from + (opposite) as electrons are negatively charged

In my opinion, just remember electric fields moves from positive to negative and this direction is positively defined. And so a positive charge will experience a positive force(same direction) and a negative charge expereinces a negative force(opposite)




Uniform electric field

So when you have two parallel positive and negative plates. There will be a uniform electric field.



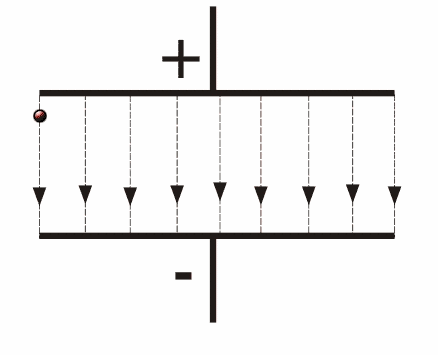
We show it by using:

• parallel lines
• Equal spacing

So when the electric field strength is constant or uniform we get the same force acting on the charge anywhere(if the same charge is used)

This is very useful as there will be calculations on the projectile of electrons and its motions because, the force or the acceleration remains constant.



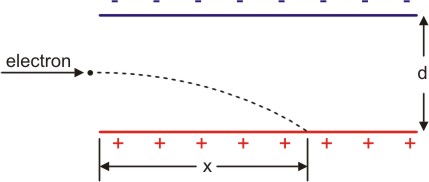
So we can calculate the force acting on the charge and find the acceleration

Acceleration = Force/mass

Usually the weight of the electron is very small so we neglet it and we just use the electro static force.

So after finding the acceleration, we can use the 4 equations of motion to predict the electrons projectile

This is very similar to like a ball being thrown and predicting its motion




Uniform Electric field strengths

Usually, we need to calculate the electric field strength caused by two plates. When we connect the two plates to a circuit one plate becomes positive and the other one becomes negative.

So usually the higher potential will be positve and the lower potential is negative.

So we can calculate the potential difference between these two plates like the below one



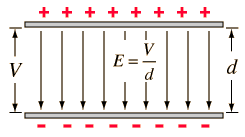
The magnitude of this potential difference and also the seperation d of the two plates will determine the electric field strength

E = ∆V/d

To make it simpler, just take the difference in potential differences and divide it by d. And always remember electric fields are from the higher voltage to lower voltage.

For example, one plate has a voltage of 100v and the other one -100v, both were separated by a distance of 10mm. Find E

E = ∆V/d

E = 100-(-100)/(10÷1000)

E = 200/(10÷1000)

E = 20000Vm^-1

Linking these 2 Equations

E = F/Q

E = ∆V/d

Both have the same E

F/Q = ∆V/d

So by knowing the potential difference and the distance we can find the force acting on a particular charge

F = QV/d

And thus find the acceleration




Work done

To calculate the work done by the electric field on the charge is very simple and we know:

Work done = Fs

So using this equation:

F = QV/d

We can get :

Fs = QV

In fact, the work done by the electric field on a charge is QV

This is also an important truth as work done in circuits is same as:

Work done = eV

Because emf is defined as the work done per unit charge

There is another way of calculating the work done by the electric field and that's by checking how much Kinetic energy the charge has gained.

This requires the equations of motion to calculate the final speed and all which is quite complex.

It's much easier to use

W = QV

But remember, this is the work done in order to move the charge from one plate to another. So if we need to find the work done to move a charge from the center to one of the plates we need to half the work done by the equation.

Lastly, this idea of eV is heavily used in radioactive physics as it is the work done when an electron moves in a potential difference of 1 volt. This is known as electronvolts and this also measures energy.




Back Next



Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...




End of Chapter Questions

Collection of Topic Questions to understand the topic more.


Try out




End of Chapter Videos

Collection of Videos to Support Your Understanding.

Remember these videos are handpicked by me and I feel these are the best ones out there. But I constantly update this list for each chapter. The Youtubers are more than welcome to contact me.

Also, don't forget to Subscribe to our Youtube channel - MrWik


Watch