Energy, Power & Efficiency

The Basics

We define energy as the abilty to do work. This might seem very misleading because, we can waste alot of energy without doing proper work. We will see below what is work done! Also you need to know that Energy is not a thing but, a concept in Physics. We can not prove that energy is always conserved, we just believe it!

SI Units: Joules (J)

Law of conservation of energy

Energy can not be destroyed or created but, can transform from one form of energy to another form

Work done

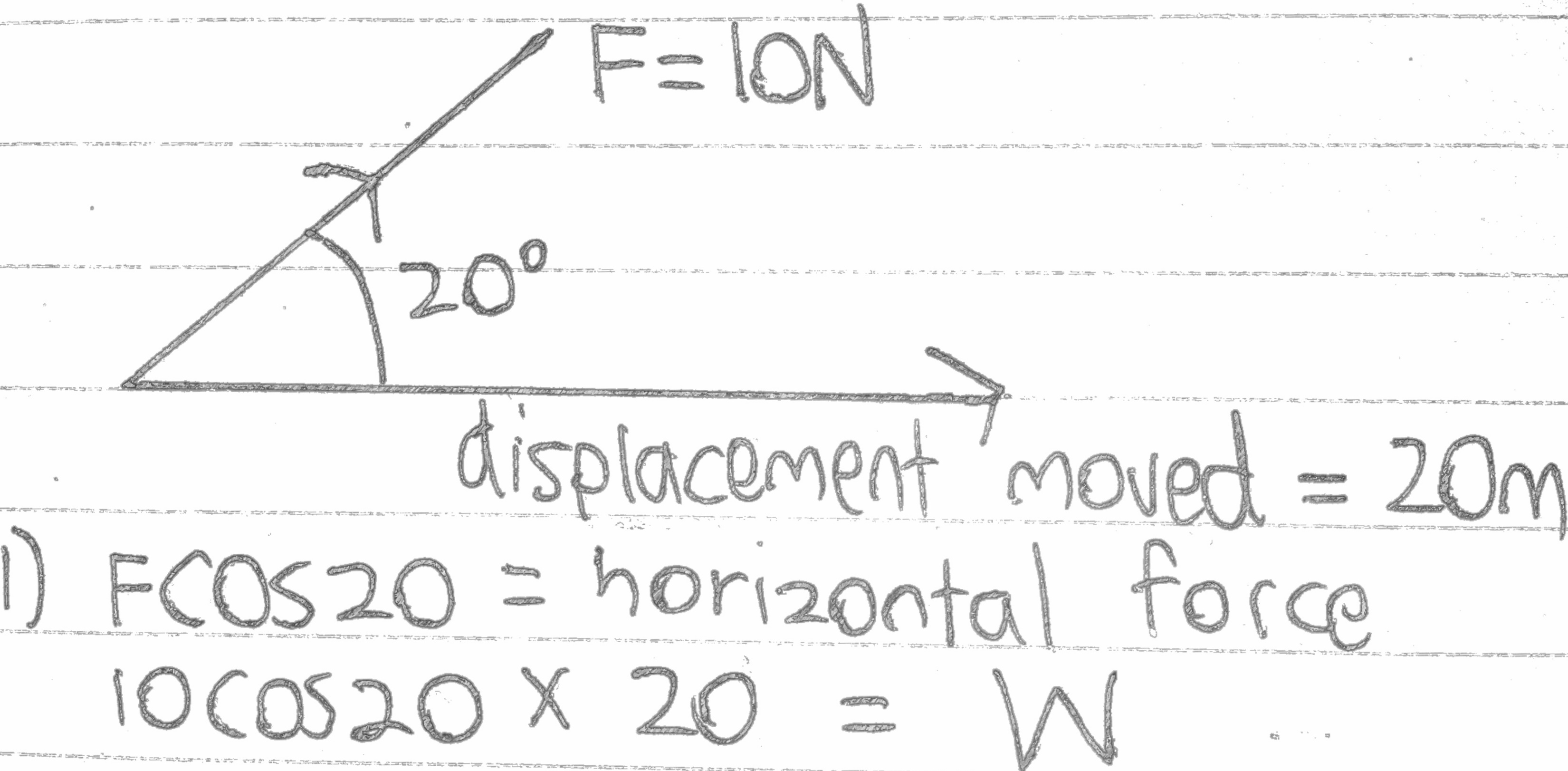
Is the force times the displacement moved in the direction of the force

Work done = Force * Displacement

W = Fs

So if we need to find the work done on a particular object, we find the force of that specific work

What do I mean by specific work? Well, let us take an example:

We carry an object from the ground to a certain height

We know that we have done work against gravity to carry the object - usually exams ask this specific work done. But when you are carrying the object, you may have done work against many other forces such as air resistance and more. We do not count this as this is called the total work done. We will see this later

Another example is the work done against friction. It is the frictional force * displacement moved

So the work done by a particular force (useful work done) is the specific force times the displacement of the direction of the force

Let us see a worked example:

Kinetic Energy

Energy possessed by moving objects

Kinetic energy = ½*Mass*(velocity)²

KE = ½mv²

Derivation is not required but, good to remember!

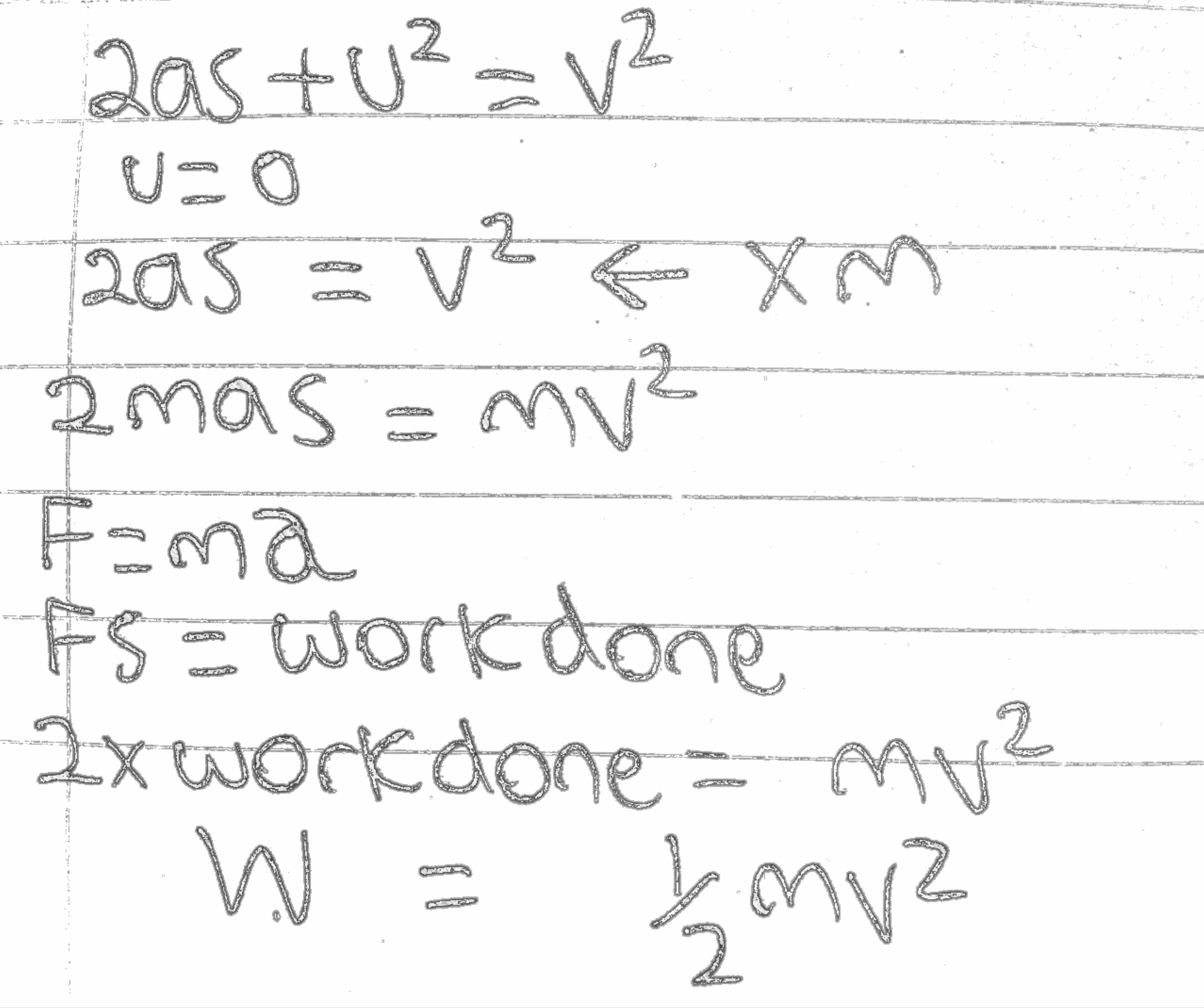
Gravitational potential energy

Energy possessed by objects in high positions

G.P.E = Mass*g*height

Gpe = mgh

So because g is usually uniform for a small change in height - 9.81 is ok

Link between GPE and KE

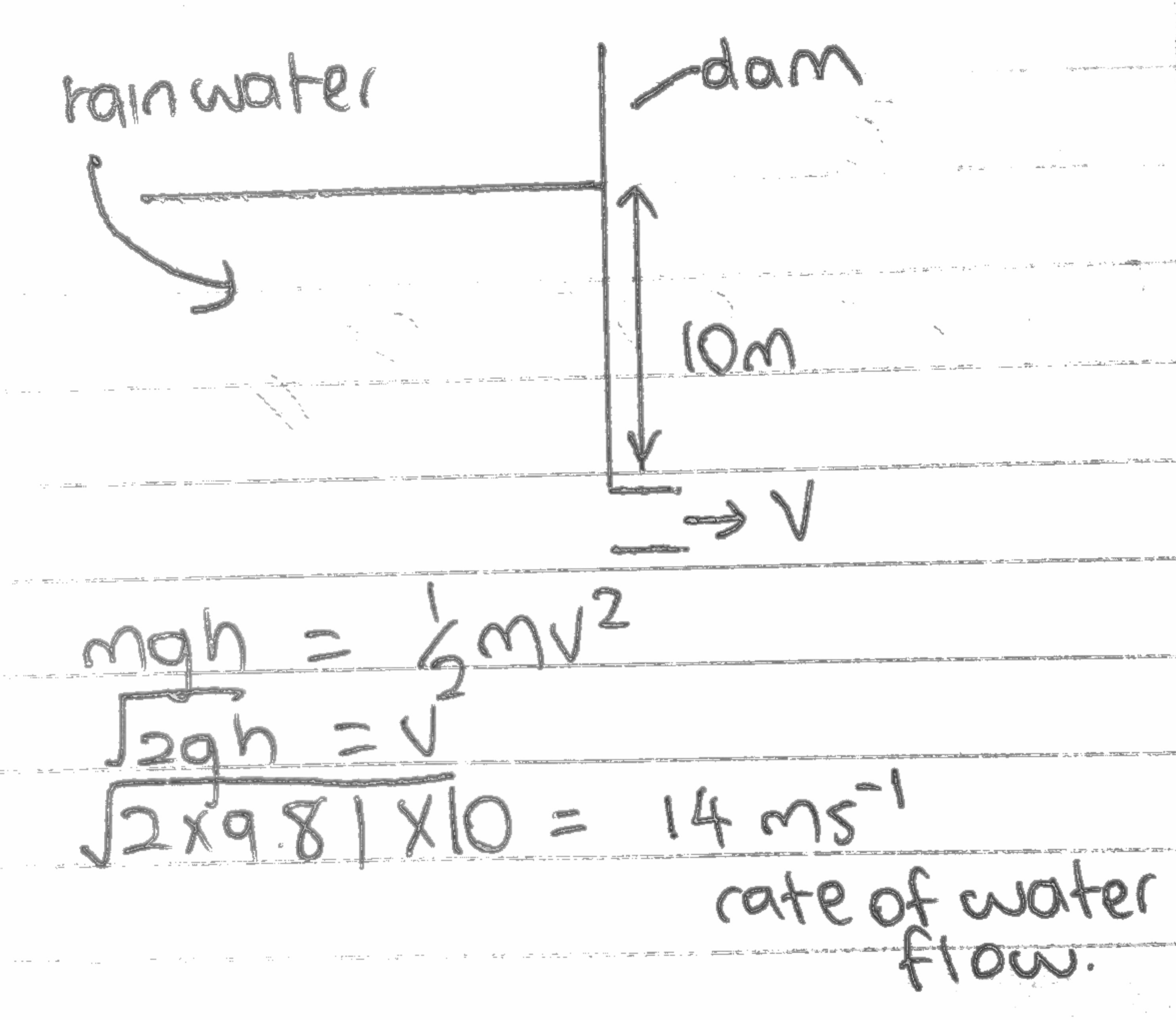
Assuming all the gpe is converted to KE, for example a ball rolling down from a high position to a lower position (100% efficient)

We can say the Gpe=KE

mgh = ½m *v²

By cancelling m both sides and making v the subject

2gh = v²

(2gh)^1/2 = v

√(2gh) = v

To equation states that when an object of any mass falls from a particular height, they will always be converted to the same velocity

Why? Logically speaking, we know that if we drop a very heavy ball and feather in a vacuum both have the same acceleration and velocity at the bottom, irrespective of their masses

Here are some examples:

And another example in the form of a pendulum:

More questions and demonstrations

This chapter requires a lot logic and so we will ask you to watch this recommended video by Revise Zone to understand the topic more.

Power

The rate at which work is done or energy is transformed

SI units: Watts

We use Watts as the units instead of Js^-1

Power = Energy/time

or

Power = Work done / time

P = W/t

There are actually alot of equations for power

Energy transformed is the same as work done - for example, if we push an object, we move the object using chemical energy, so energy is actually transformed from one form to another!

Work done = Energy transformed

However, we usually consider the useful work done because more work is actually used. This is because, nothing is fully efficient. So the power we need to do the specific work get is called Mechanical power or required/useful power

The total power is always higher!

Efficiency

It is a very straight forward concept and it shows out of the total work done or power what percentage is useful

Efficiency = useful workdone/ total work done

Efficiency = useful power/ total power

Efficiency is usually expressed in terms of percentage so we multiply by 100

Efficiency = (useful workdone/ total work done) * 100

So this is how the exam will ask the question

The efficiency of the system is 30%, The elevator carries a load of 1000N for 2m for every second. Calculate the total power?

So that energy we have to calculate is actually the total power, so it is pretty straight forward. Just make the total power the subject

The mechanical power is the power required to do the work

W = Fs

P = W/t

As it is for every second, the work done is equal to the power

1000*2 = 2000J every second

Then use the efficiency equation and make the total power the subject

Power of a constant velocity

By law, we don't need to supply energy to keep an object moving in a constant velocity but, in day to day life, we need energy to keep an object moving at constant velocity as there is frictional force acting on the object. For example, if a car was moving at constant velocity (say top speed). We need to keep on pedalling the engine, so the engine provides a constant power

Power at a constant speed is given by:

Power = Force * Velocity

P = Fv

The force used could be the friction or the engine thrust as both are same!

This shows the power done by the engine is converted to heat ONLY and not to kinetic energy

This is actually an important conversion in terminal velocity - the energy is converted to heat only.

If it's accelerating, it's converted to both KE and HEAT

Watch out! They might ask it in different ways.

Work done by Gases

We know that gases can exert pressure and so they apply a contant force per unit area.

Let's take the below gas syringe:

It has some pressure greater than the atmospheric pressure. Logic tells us that the gas syringe should expand until the internal pressure is equal to the outer pressure. In other words, the outer force must equal to the internal force as the area is same.

So when the volume increases, a force is exerted for a particular displacement

Work done = Fs

Force = Pressure * area

Workdone = Pressure * area * s

Workdone = Pressure * change in volume

W = P∆V

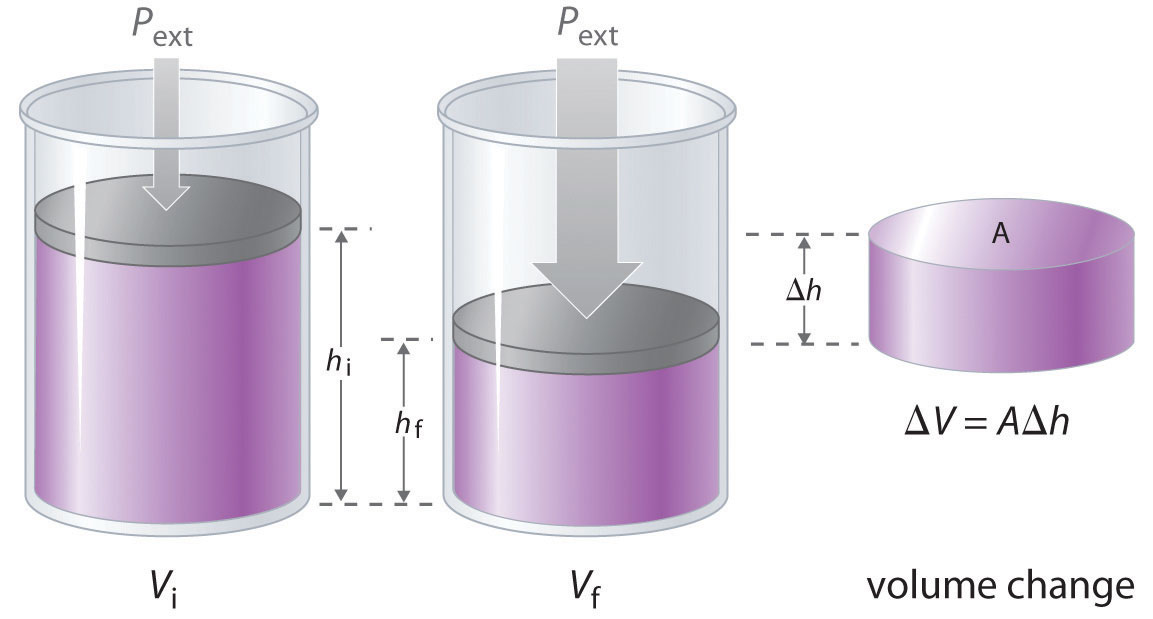
We use change in volume because, we take the change in displacement.

So what is this pressure?

Now for the gas syringe to expand, it must do work against the atmospheric pressure

Pressure = 1 atm or 10⁵Nm^-2

So actually the work done by the expansion of the gas is the work done against the atmospheric pressure

For example, if a gas syringe expands by a volume of 2m³, the work done is equal to 10⁵ * 2 = 200000J

Remember that volume is in m³

Another point to remember is that this is the energy required just to expand the gas ONLY. Not to push any weight or mass/accelerate. So if there is a mass on top. Work done on rising the mass and the expanding the gas is more.

Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...