Physics(9702) Practicals - Tips to get fullmarks

Basics

Truly for you to master the practicals you must look at some past papers. That's why I have given a list of past papers below!

However, there are somethings and points you need to remember

Follow the instructions

The instructions are quite straight forward and basically explains the whole process. You need to identify what is being changed and what is being measured. This is important as this gives us an idea of what is supposed to change

Significant figures

The marksheme for the practical paper has strict marks for significant figures

If you took a measurement and you're suppose to record it, we need to give it to the precision of instrument used or given

Here is a list of the decimal places you must leave the value in for each instrument

Name	Decimal places
Ruler	1 d.p in cm
Meter ruler	1 d.p in cm
Micrometer	2 d.p in mm or 3 d.p in cm
Vernier calliper	Depends - See below
Stopwatch	2 d.p in seconds
Weighing scale	Depends - follow the scale

So the above table tell us how many decimal places a reading must be left in for each instrument used

Also a point to remember. If they give 2 marks to obtain a particular value, it means they give marks for averaging also

For example, they might ask to find the diameter of the wire using the micrometer so we must take atleast 3 readings and find the average

The next part they ask is the percentage uncertainty and there are some misconceptions about this part. We will discuss it below!

For the experiment:

They will give a table and ask us to get 6 different values (make sure you do 6) for the independant variable

We might have to calculate some values for the dependant variable. The calculated value must be given in the lowest Significant figure of the recorded raw data used in the calculation

For example, if we need to find density and the mass is given to 2 S.f and the volume to 3 S.f, then the density is given to 2 S.f

They usually ask this question directly:

Explain how many significant figures should the density be given in

You must state that we must use the lower of the significant figures of the raw data used and also state the raw data used are the mass and volume.

And say the one with the lowest significant figure is for the mass which is 2 S.f. So we record the density in 2 S.f

Note how I stressed the word recorded data. This is because, this method only applies for recorded data. If we use a constant in a calculation, it won't affect the final reading S.f - Let's see an example

The Current(A) is 0.333A. What is 1/A?

The reciprocal of A must also given in the same S.f of 3

Another example is when we find the period, we usually find the time for 10 Oscillation(this is required) and we get(example) 13.23sec

To find the time for one oscillation we divide it by 10 and this become 1.323 sec, it must follow the same S.f - So please remember this!

Another point is that the S.f of a field or column must be consistent(which naturally happens, if you follow the above rules)

Taking readings

When taking values for an experiment, we must change the independant variable and make sure they cover a large range such as taking the maximum and the lowest reading.

The values for the independant variable must be evenly spaced

For example, if we allowed to take a max mass of 200g and a min mass of 50g. The difference is 150g. Then divide it by 5 so then we know the mass should increase by 30g for every trial.

50g, 80g , 110g, 140g, 170g, 200g

This uses the maximum range possible and it is also evenly spread.

If you can't get an even spread, try rounding it to the nearest value which can be read

Table

They will ask you to record 6 values which means 5 additional values because, you already recorded one at the start of the paper

Make sure the heading includes the name and also the units

The data in the table should not have the units

Make sure you follow the significant figure rule

Graph

They will ask you to plot the graph using the values from the table. Make sure you follow the instructions

Use small crosses to plot the points

Label the axis with the correct units and names

Make sure you use a good scale of multiples of 2 , 4 , 5 or 10 - Never use 3 or 9!

Make sure the scale is marked and don't leave anything blank - (Example if we start from 20 and it goes until 30, then mark 22 24 and 26 and 28)

Usually we must be able to determine the line of best fit. This is done by drawing the line which passes close to all the point (this can be cleverly manipulated!)

The markshemes only accept one anomolous point which must be circled and labelled. So make sures other points are very close to the line

How close should the points be depends on the marksheme

Gradient

Finding the gradient is easy

Y₂-Y₁/X₂-X₁

The process of finding the gradient must be shown. So we need to show dotted lines and draw a dotted triangle

Take two points in the graph and make sure it occupies more than half of the graph!

Find the gradient using the above equation

Units are not required for gradient

Then after find the gradient, they will ask you to find the y Intercept (c)

Use this equation

y = mx + c

C is the Y Intercept. To find this we need to substitute a x value and a y value (which is part of the line of the graph) and the gradient (m) which you found and find C

C has the same units as the Y variable

Base units and Constants

Most of the time, some questions gives us the equation in a different form which can be linked with the original y = mx+c

By using this equation, we can find the constants in the new equations

y = 2ax + z

Is same as:

y = mx + c

To find a and z:

By comparing with the original equation, we can see that z is the same as c and that 2a is equal to the gradient (m)

By equating these, we can find the values but, questions are trickier than this

The units for a and z can be found by the same way and must follow the original equations

Proving Relationships

Sometimes they ask to do an experiment and find whether the relationship is true or not

For example:

T ∝ √L

They will ask to calculate the constant K for two or three different independant variable values

This is done by

T/√L = K

We must follow the significant rule and record K in the lowest significant figures. Also they might ask to explain this!

Now usually due to many other factors such as random errors and human error, the values of K would not be exactly the same. Sometimes it could be very different but, what must be the criteria used to check if the constants calculated are actually the same(within experimental accuracy) or not?

Take The difference between the two values of K and divide it by the lowest K value

For this particular calculation, K can have more significant figures, if you want to make it more accurate

(K_max-K_min)/K_min

You must clearly state this criteria:

- The Percentage difference between the two K values are greater than 10 % and so this shows that the constants are not within experimental accuracy. Thus, it shows that the relationship or hypothesis is not true

If it is within 10%, then you should say:

As the percentage difference is less than or equal to 10%, it is within experimental accuracy and so the relationship is be true

Improvements

In my opinion, this is the hardest part of the paper as they ask to identify the errors and the improvements for each error

This usually depends on the experiment but, I will discuss some errors which are common in markshemes

1. Two values of K are not enough to make a conclusion - so you must take more values and reading and plot a graph to see if it is a straigth line

2. If the experiment is measuring time ( like the period ), you can say it is difficult to determine the end and the start of oscilliation - so you can either use a fiducial mark or use a larger length of wire or use a video camera and a timer in the background to find the period more precisely

3. This is for oscillations, you could say the oscillations dies off easily - we can use a lead bob or switch off the fans and close the windows

4. If the Experiment included measuring a height or measuring length, then you can say that the length was not measured accurately - The improvement is to measure the length between the centre of masses and this may need a micrometer. Or if they ask to measure the height, we can be consistent with the results (such as reading it from the same point)

5. If the experiment includes dropping something, the object may had sideway velocities from the hand. so we can use an electromagnet as an improved version

There are actually many things you can comment on but, just remember these points. Difficulty in reading, lack of results, external factors, using non precise instruments (use sensors instead)

Micrometer and Vernier calliper

We will discuss on how to use them. Also this might come in MCQs and Theory!

• Micrometer

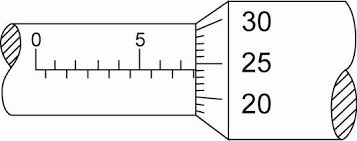
Make sure that the object is between the jaws of the micrometer. First read the main scale which is in millimeters

The main scale is read to the nearest 0.5mm

Then take the fractional scale which is from 0 to 50. This scale must be multiplied by 0.01mm

The point where the fractional scale is aligned with the main scale, read it and multiply it by 0.01mm and add it to the main scale

Reading = Main scale Reading + (Fractional scale Reading * 0.01)

This gives the final value in millimeters!



• Vernier Calliper

In practice, the smallest value is given in the instrument

In MCQs, this must be calculated

The main scale is usually given to nearest 0.1cm and sometimes the secondary scale can have either 10 or 50 divisions

If it is 10 divisions then the smallest reading is 0.01cm

0.01cm = 0.1/10

If there is 50 divisions, then the smallest reading is 0.002cm

0.002cm = 0.1/50

Notice that this is in centimeter and so the final value is given in Centimeters

Final reading = Main scale + (Sub-scale * smallest reading)



Zero error

Usually when the jaws of the micrometer or the vernier calliper are closed it must read 0

In reality, this is not the case and sometimes there could be positive or negative zero errors

So after finding the zero error you need to adjust the readings you get

Zero errors must contain the sign to indicate if it's positive or negative

I will talk about negative zero error only as it is a bit difficult



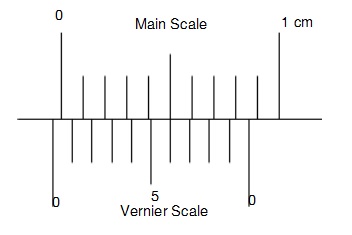
So we can see that the vernier scale is behind the zero mark. This shows it's a negative zero error

The vernier scale aligns at the 6th mark so this means 0.06cm. However, this value is not the answer. If it is a negative zero error we must take the remaining divisions which is 4 (10 -6) so we get 0.04cm. So the zero error is - 0.04cm

The reason for this is that the 0.06cm is more from the -0.1cm mark(imaginary) this gives us -0.04cm which is the zero error!

The reason why we include the sign is that whenever it is a positive zero error, we reduct it from the measured reading to get the final value

If the zero error is negative, we add to get the final reading

Final reading = Measured reading - ( Zero error )




Absolute uncertainty

Honestly, these topics are hard to explain digitally but, I will go through them briefly

In all instruments such as the ruler there is a minimum value which it can read. For example, a ruler reads to the nearest 1mm or 0.1cm

Half of this is 0.05cm

This is considered to be the absolute uncertainty for a single specific reading

However, we take the reading twice because, we find the change of length from the 0cm so the absolute uncertanity is the same as the minimum value of 0.1cm

This applies for all instruments, like for burettes - the minimum value is 0.05cm and so the absolute uncertainty is 0.1cm because. we take two readings when finding the volume

However, if we take the value of the temperature , it will have a minimum value of 1°C and the absolute uncertainty will be 0.5°C not 1°C as the value is taken only once

Remember that absolute uncertainty is not the same as the minimum reading. Sometimes it could be different or the same depending on the instrument




Relative Uncertainty and Percentage Uncertainty

This is simply the ratio between the absolute uncertainty and the reading

Relative uncertainty = Absolute uncertainty/Actual reading

Let's take an example. We measure using a 10cm ruler. what is the relative and percentage uncertainty?

0.1cm/10cm = 0.01

This is the relative uncertainty. To find the percentage uncertainty or the percentage error, just multiply the relative uncertainty by 100

1% = 0.01 * 100

Percentage uncertainty is very important especially when we need to find the percentage uncertainty for the final value

Also it's better to use percentage uncertainty as it makes calculations more easier

Absolute uncertainty when adding and substracting

Usually when doing calculations and the two values contain absolute uncertainties, to get the final absolute uncertainty we just need to add both of the absolute uncertainties

Absolute & percentage uncertainty when multiply by a constant

When a reading containing the absolute uncertainty is mutiplied or divided by a constant, the absolute uncertainty is multiplied or divided by the same amount

For an example, if a reading of 10cm with an absolute uncertainty of 2cm is divided by 10 then the final value is 1cm with an absolute uncertainty of 0.2cm

Also keep in mind that percentage uncertainty doesn't change when you muiltiply it by a constant like π

Percentage Uncertainty when Multiply/Dividing two or more readings

If a reading which contains an uncertainty is multiplied or divided with another value which has an uncertainty, you just add the percentage uncertainties together

This is why I said to use percentage uncertainty as in calculations it's much easier

Absolute Uncertainty in Averaging

This is very important and it goes to the point above where I mention that they ask to find the percentage uncertainty of a reading for a micrometer or vernier calliper

Many people think that you need to guess it but, there is a clear and easy method

As you did take atleast 3 readings, find the maximium reading and the minimum reading from the set of values

Then divide by two

Max reading - Min reading / 2

This final value will give the absolute uncertainty, then find the percentage uncertainty by dividing the absolute uncertainty with the averaged value (averaged recorded reading) and multiply it by 100

This is way easier




Accuracy

This shows how close a reading is to the actual value

For example, many MCQs will give a range of values and ask whether it is precise and accurate

The values are accurate if they are close to the actual value - For example we know g is 9.81 but, the values state 9.82, 9.80, 9.80 and so on, this is accurate as it is close to 9.81

The accuracy really depends if the experiment has systematic errors which are errors in the plan or set up of the experiment which affect each reading by the same amount and this can't be removed by averaging. This includes zero errors or scale errors so each reading is wrong by the same value




Precision

This is the difference between the highest value and the lowest value in the set of values/readings

In other words, if the difference is less, it means the readings are close together and more precise

This really depends on the random errors of the experiment which are errors which readings are affected by a random factor and can be reduced by averaging. These include changes in the enviroment, reaction time and parralax error

Let us take the same set of readings - 9.82, 9.80, 9.80

By judging we can clearly say these results are close together and so they are precise

And a further point is that these values are also accurate as the average is 9.81

In fact, accuracy and precision has no exact terms but, is a measurement of the degree of accuracy and precision




Here are some practice questions for you to try out. These are some of the physics practical papers. It's always good to try out some more past papers! They all have the same pattern, so if you master the above steps you can easily get full marks for your exams

1st Practical paper

2nd Practical paper

We have come to the end of the Physics AS level syllabus of Physics 9702. The A level Section will be coming soon so until then, try out some past papers and watch the recommended videos!



Back



Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...




End of Chapter Questions

Collection of Topic Questions to understand the topic more.


Try out