Velocity, Acceleration & Motion Graphs

Distance

It is the length moved by the object irrespective of its direction

SI Units : Meters (m)

Displacement

It is the distance moved in a specified direction from the point of reference // It is the shortest distance between two points.

SI Units : Meters (m)

Velocity

It is the rate of change in displacement

ms^-1 = m/s

SI units: Meters per sec ( ms^-1 )

What is velocity?

Remember velocity and displacement have a sign/angle and a magnitude

Whenever we talk about velocity it means instantaneous velocity or velocity at a specific point. So remember to say "rate"

Velocity = Change in displacement / Time

v = ∆s/t

For Displacement-time graphs, it shows how displacement of an object changes with time. Displacement is the distance from the starting point (in a specified direction)

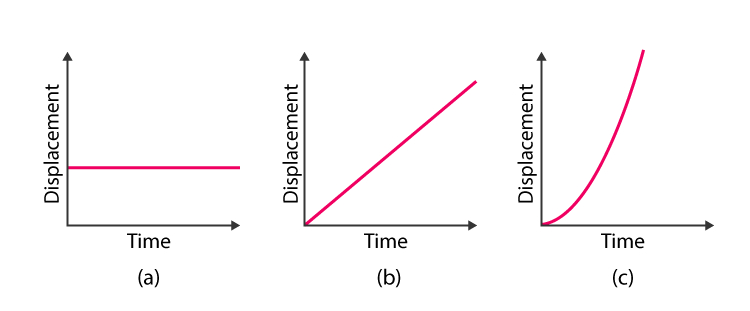
The gradient gives us the velocity

Gradient=(Y₁-Y₂)/ (X₁-X₂)

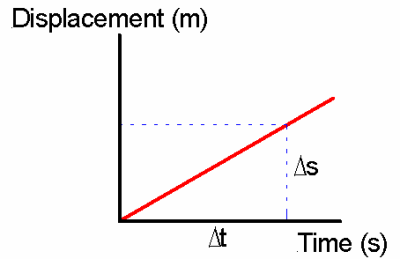
so the change in y gives us the change in displacement and change in x gives us change in time, so this gives us velocity

If the displacement-time graph is curved this shows that the gradient is changing, so when the gradient is changing the velocity is also changing which means the object is accelerating

Also remember these points, displacement is a vector and can have negative values. If it is behind the starting point. Whenever the object is losing velocity the gradient becomes horizontal. As soon as the object moves behind, the gradient is negative and so is the velocity. This is because we look at instantaneous velocity and so the rate of change in displacement is now negative becuase it is in the opposite direction. So the displacement value decreases but, if it hasn't still passed the starting point, the graph is still above(positve)

For curves, you have to find the velocity at a particular time so we need to draw a tangent of the displacement-time graph

The area under the velocity-time graph gives us the NET displacement

Speed

It is the rate at which distance changes

Speed = distance / time

ms^-1 = m/s

SI units: Meters per sec ( ms^-1 )

Remember that average speed and instantaneous speed is different as average speed is the total distance/displacement travelled per unit time so it is not rate but an average

The speed-time graph is very similar to displacement-time graph however, the negative gradient part doesn't exist in speed-time graphs. The gradient is equal to speed

Also the graph can not have negative gradient or speed as speed is a scalar quantity

Acceleration

It is the rate of change in velocity

Acceleration = change in velocity/time

a = v-u/ t

This is actually one of the four equations of motion

(Acceleration*time) + initial velocity = final velocity

at + u = v

So remember, whenever velocity changes, there is always an acceleration

Negative Acceleration

Whenever an object is slowing down in the positive direction then we know final velocity(v) is less than the initial velocity(u). So then we get a Negative acceleration. However, if we were to increase the velocity in the same(positive) direction, it is a positive acceleration

When an Object is increasing velocity(magnitude) in the opposite direction, it has a negative acceleration. This is because, it becomes -(v-u). If it were to slow down then it would have a positive acceleration

Equations of motion

Remember these equations only work when acceleration is constant. When acceleration changes then we need to break it to separate(fixed) accelerations and substitute the equations separately!

Memorise these!

at + u = v

2as + u² = v²

(u+v/ 2) * t = s

½at² + ut = s

Also remember these equation works for single direction motion only - basically this means contant acceleration

Just remember if you forget, U+V/2 * t is used to find the area under the velocity-time graph. It's that simple!

Projectiles and motion

Once you know how to predict the velocity, time and acceleration of an object using these equations of motion then we could apply this in projectiles/2d motions. The equations allow us to determine the velocity for a CONSTANT accelerating object in a straight line only. We need to split the (initial) velocity to two separate straight lines. This is called resolving! So if we have an initial velocity of U = 10ms^-1 which is 30° North from East then we can resolve it using 10cos(30) - Horizontal velocity and 10sin(30); - Vertical velocity.

It's better to remember, cos as closing as when the angle is closed, the horizontal component is Ucosθ

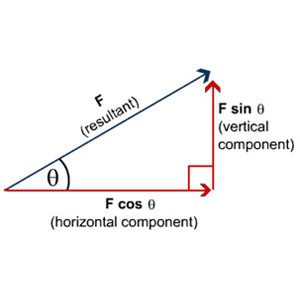
Horizontal = Ucosθ

Vertical = Usinθ

So after finding the vertical and horizontal velocity, you treat them separately. So we substitute the initial velocity to 2 separate equations

For example

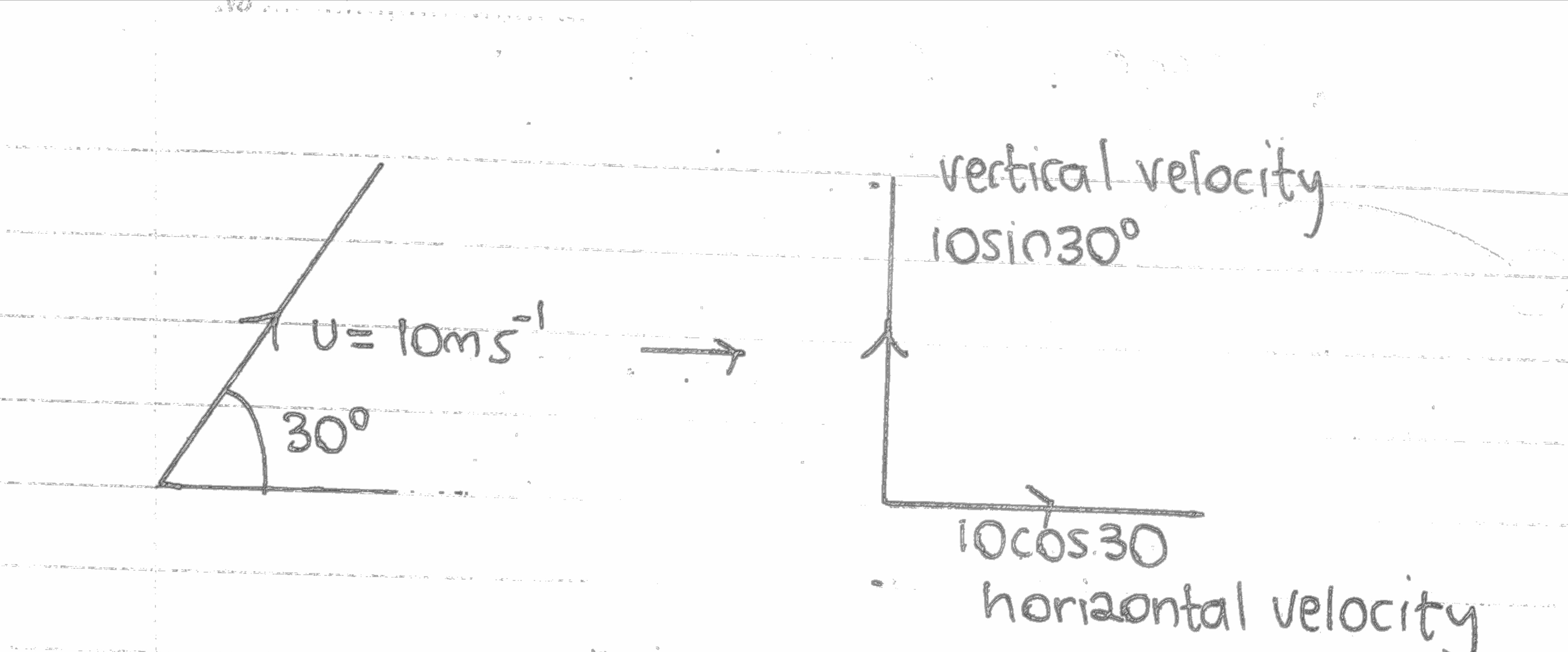
Points to remember

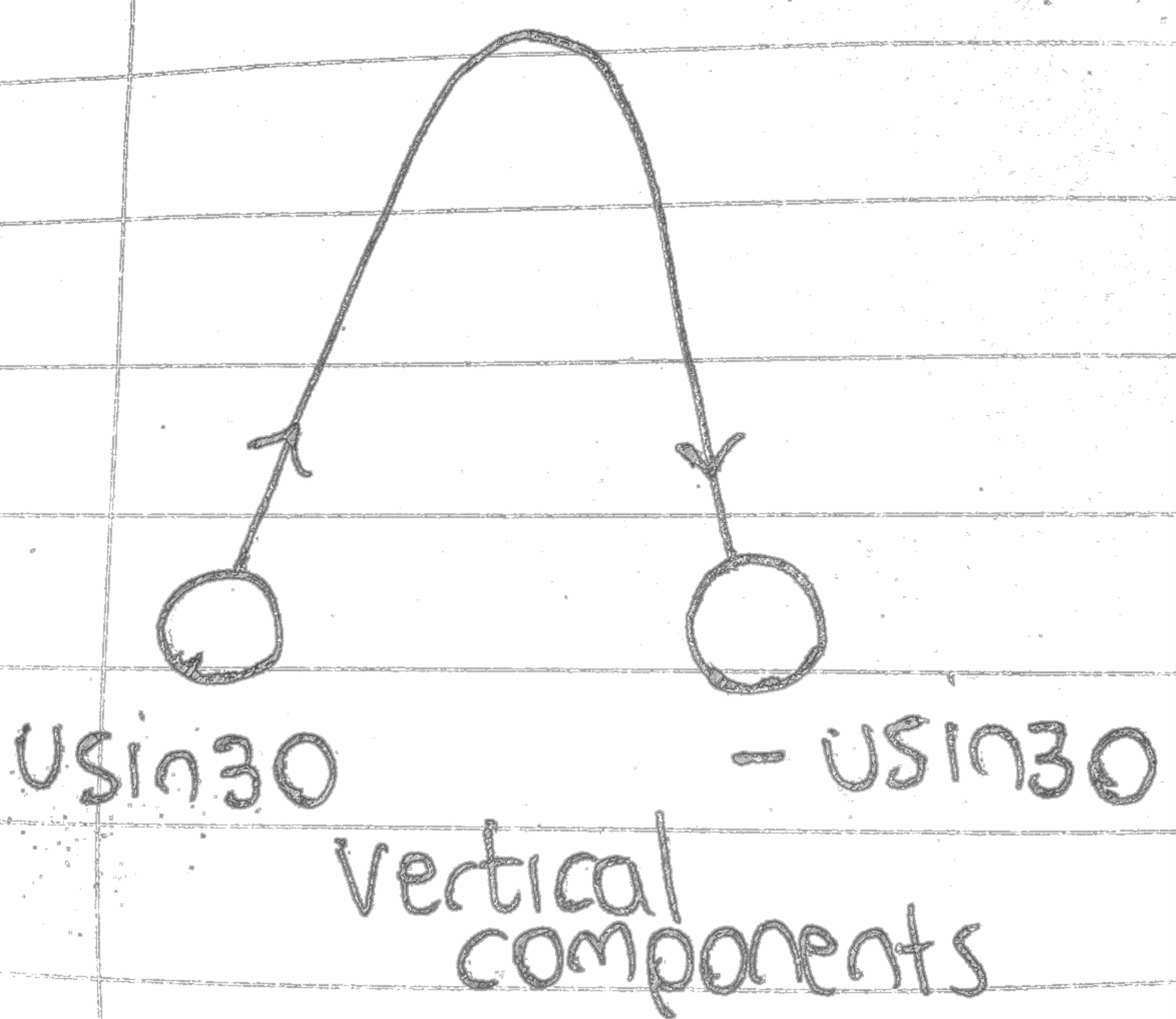
• At the maximum point/height, the final vertical velocity must be equal to zero


Why? As acceleration or gravity is in the opposite direction, it actually slows the ball until it reaches the maximum point

V_vertical = 0

To find the time? we know acceleration which is constant (-9.81). So we know (a) we know (v) which is zero and we know the initial velocity - which is Usinθ

so we could use this equation of motion:

u + at = v

usinθ + 9.81t = 0

So find t !

This gives us the time to reach maximum height/peak

• The vertical displacement of an object in the same level are equal to 0

When at the same level or height, the vertical displacement is obviously 0m. So we want to know the time for a ball to come back to the same level

½at² + ut = 0

So as we know a and we know u and we also know s which is 0m

9.81t²+usinθt = s

So this is a quadratic function and you must put this in the calculator. So go to EQN and mode 3 and put this and solve t. T(time) will have two value - Either 0 or another value. This is because, when T = 0 the object is also at a height of 0m at the start.

• When the projectile is symmetrical, remember that the vertical velocity at the end(same level) is equal to negative usinθ

You can skip this part if you want but, it is good for fast checking. This is because, when we reach the maximum point we know v = 0 when it comes back to the same level, the velocity has increased downwards and is same as the initial velocity but, negative

So then we could use → at + u = v to find t faster

Usinθ + 9.81t = -Usinθ

usinθ + at = -usinθ

-2usinθ/a = t



This is a fundamental mechanics equation

So after finding the time

We know that time is common for both the vertical and horizontal velocity. So once we know T, we can find the range or horizontal Displacement moved.

Rememebr that the horizontal velocity is not affected by any force and if there is no resultant force, there is no change in velocity

S = Ucosθt

The Ucosθ is the horizontal velocity so you can just multiply by T to find the displacement/range

We need to note that the horizontal velocity is constant always as there is no acceleration in that particular direction.

How to calcultate acceleration of free fall (g)

Do the experiment below:



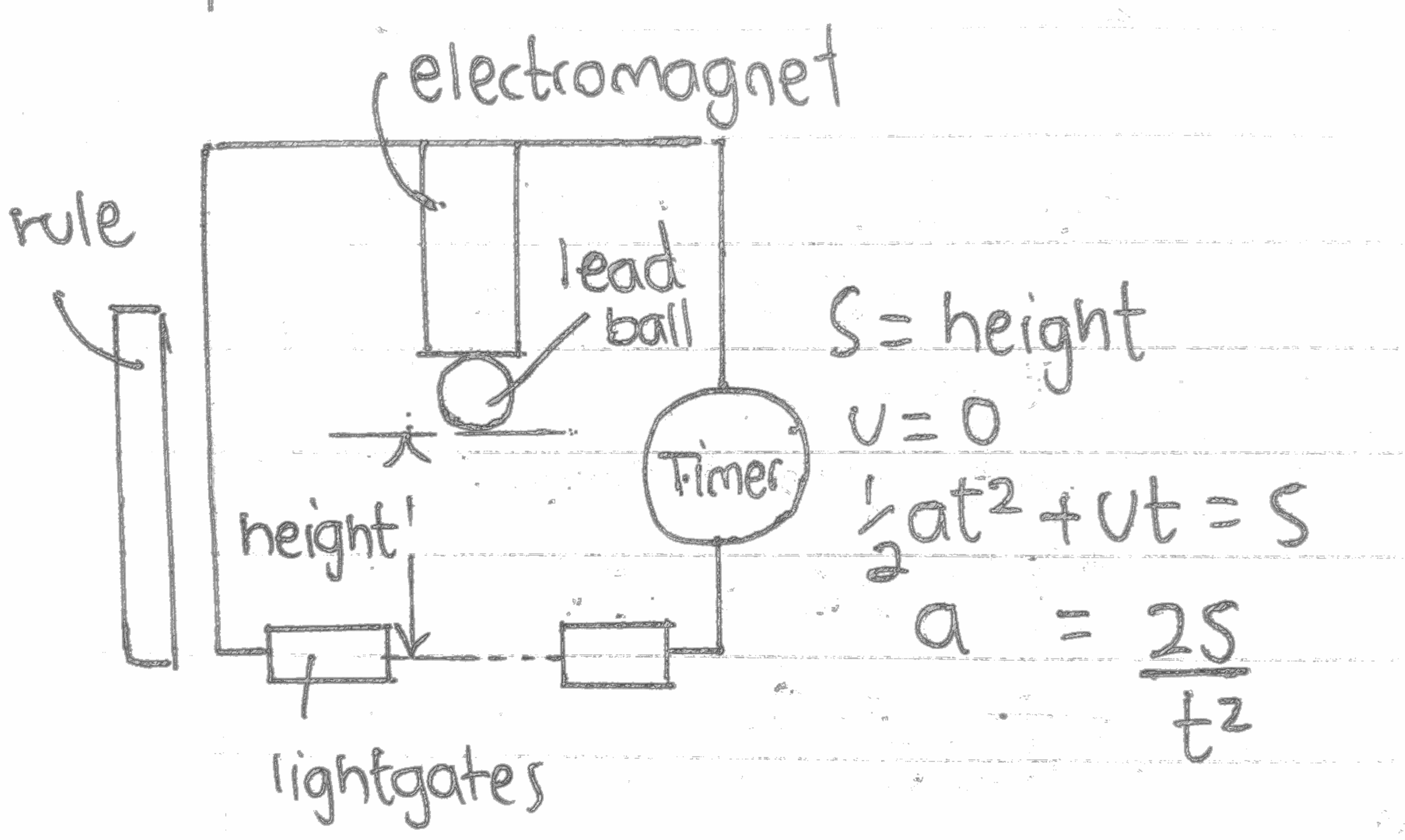
The timer starts as soon as the electromagnet is switched off and stops as soon as the ball cuts the light gate. The timer must be accurate to 0.01s

So the length is the distance from bottom of the metal ball to the lightgate.

Make sure you repeat the experiment and get an average value for time and length.

So then we can use the equation to calculate g

½at² + ut = s

As u = 0

½at² = s

So we have to plot a graph of s against t²

½at² + ut = s

Is same as the straight line equation



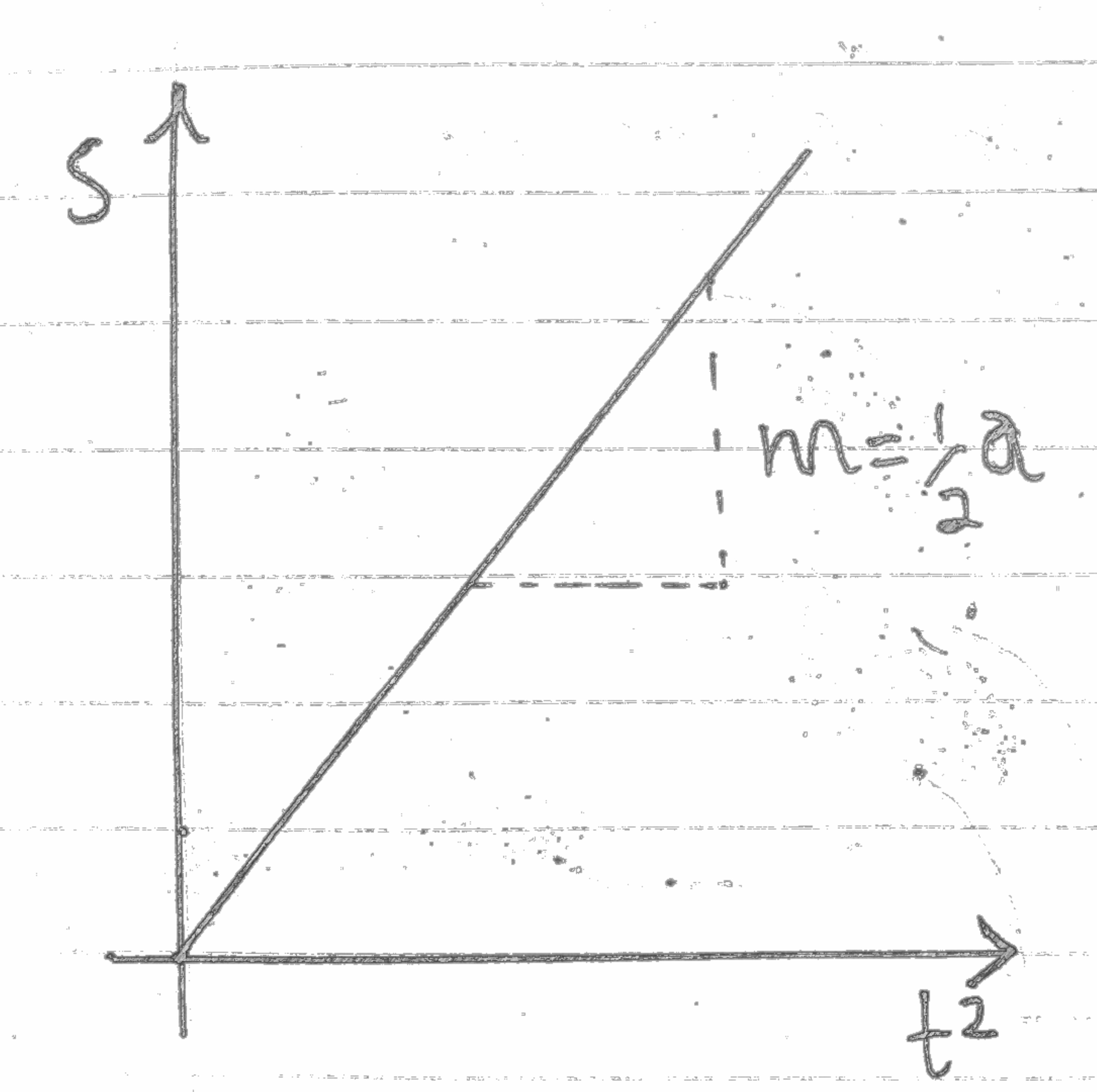
mx + c = y

The gradient is half of the acceleration so gradient must be multiplied by 2 to get the acceleration

2m = a




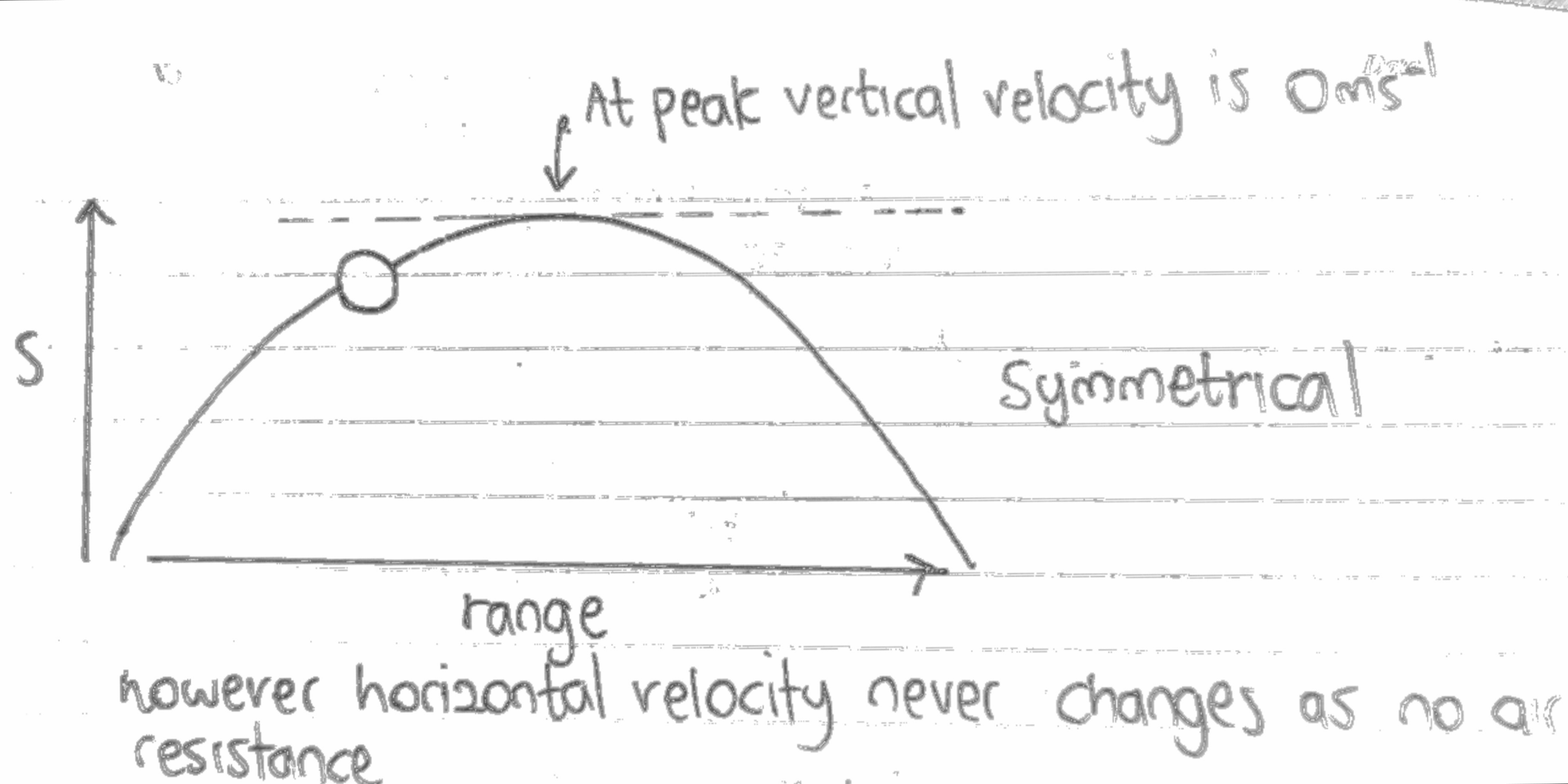
Falling under Gravity Graphs



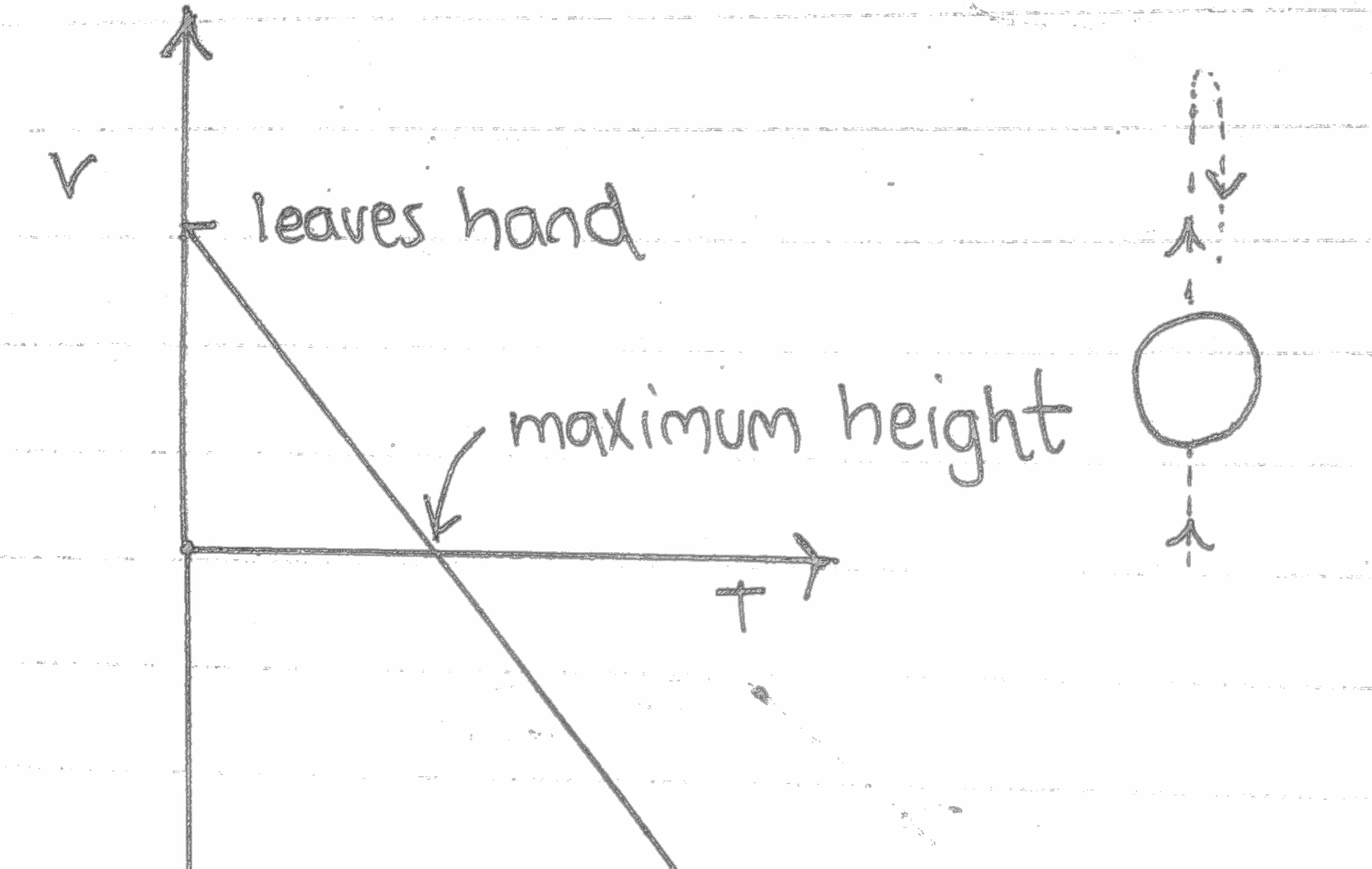
When we throw a ball up, we provide an initial velocity upwards but, the acceleration(or gravity) is downwards. So the velocity decreases until it reaches a maximum height. At this point the velocity is zero. Then the velocity starts to increase in magnitude as it falls. If we were to put this in a graph. The ball has an initial velocity at the start. This graph must have a negative gradient as gravity always acts downwards ( Negative ). And so it passes v = 0 and then continues to go downwards in a straight line!

If we drop from rest meaning at 0, then the initial velocity will start from the 0 point

Here is the displacement-time graph:



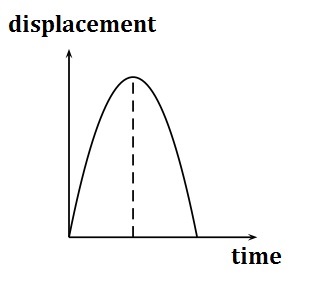
The peak is the maximum height of the ball from the the rest position/starting point.




Back Next



Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...




End of Chapter Questions

Collection of Topic Questions to understand the topic more.


Try out




End of Chapter Videos

Collection of Videos to Support Your Understanding.

Remember these videos are handpicked by me and I feel these are the best ones out there. But I constantly update this list for each chapter. The Youtubers are more than welcome to contact me.

Also, don't forget to Subscribe to our Youtube channel - MrWik


Watch