Vector & Scalar Additions & Equilibrium

Remember these!

These are the ways the exam expect answers from you:

They will ask

What is the difference between a vector and a scalar?

Vector are quantities which have a definite direction and a magnitude. Whereas, Scalar quantites only have a magnitude.

They might also ask:

Why is velocity a vector quantity and speed a scalar quantity?

You need to remember this point

Velocity is a vector quantity because it has a definite direction/sign and a magnitude whereas, speed has a magnitude only but no definite direction.

Vector examples

• Displacement
• Acceleration
• Velocity

Scalar examples

• Distance
• Speed
• Mass

Scalar and Vector additions

Scalar quantities are very easy to add. All you have to do is convert them to the same (SI)units and just add the magnitudes together. Finally, the resulting value is in terms of the same units

For example:

If a girl walks 2km North and then 4km East, the total distance will be 6 km, this is because distance is irrespective of the direction moved

Vector addition

As vectors have a direction, the direction must be considered. So there are 3 main methods of vector additions

Scaling/drawing

Please don't use this method as it's time consuming and less accurate

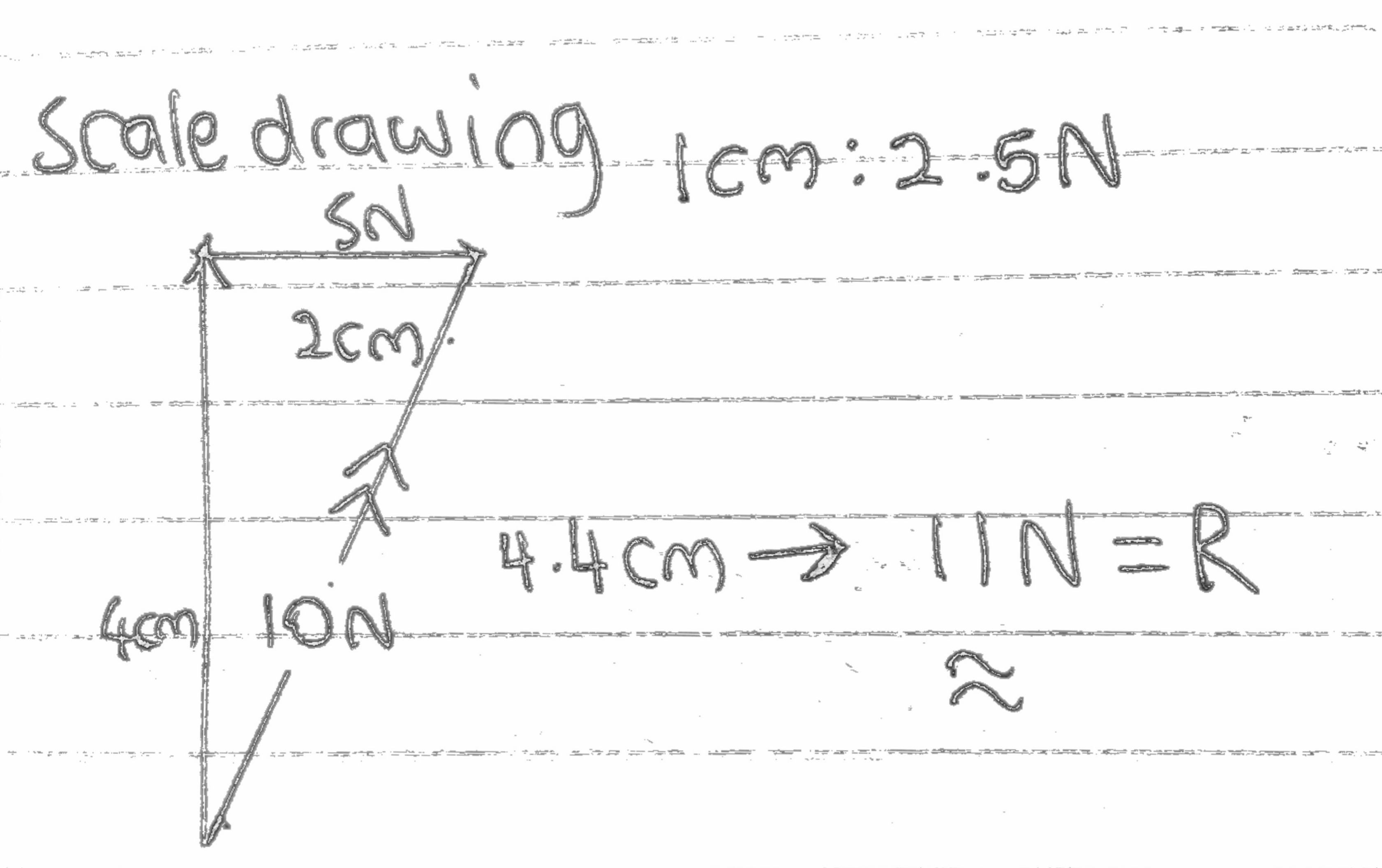
We use a key(which must be stated). Make sure you take a good and easy scale. Example: 1cm:10N. Do not use scales like - 1cm:3N. Use Multiples of 2,5 or 10

Make sure you use a good and large scale - Example - if we have a velocity of 2ms^-1. Use a scale of 1cm :0.5ms^-1

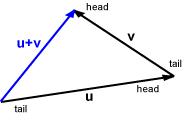
Now if there are two or more vectors that must be added, we use the Nose-tail method - Joining the Top of one vector to the back of another vector

Calculations using Cos and Sin

First of all, you must draw a sketch of the vector triangle because, you get marks for this

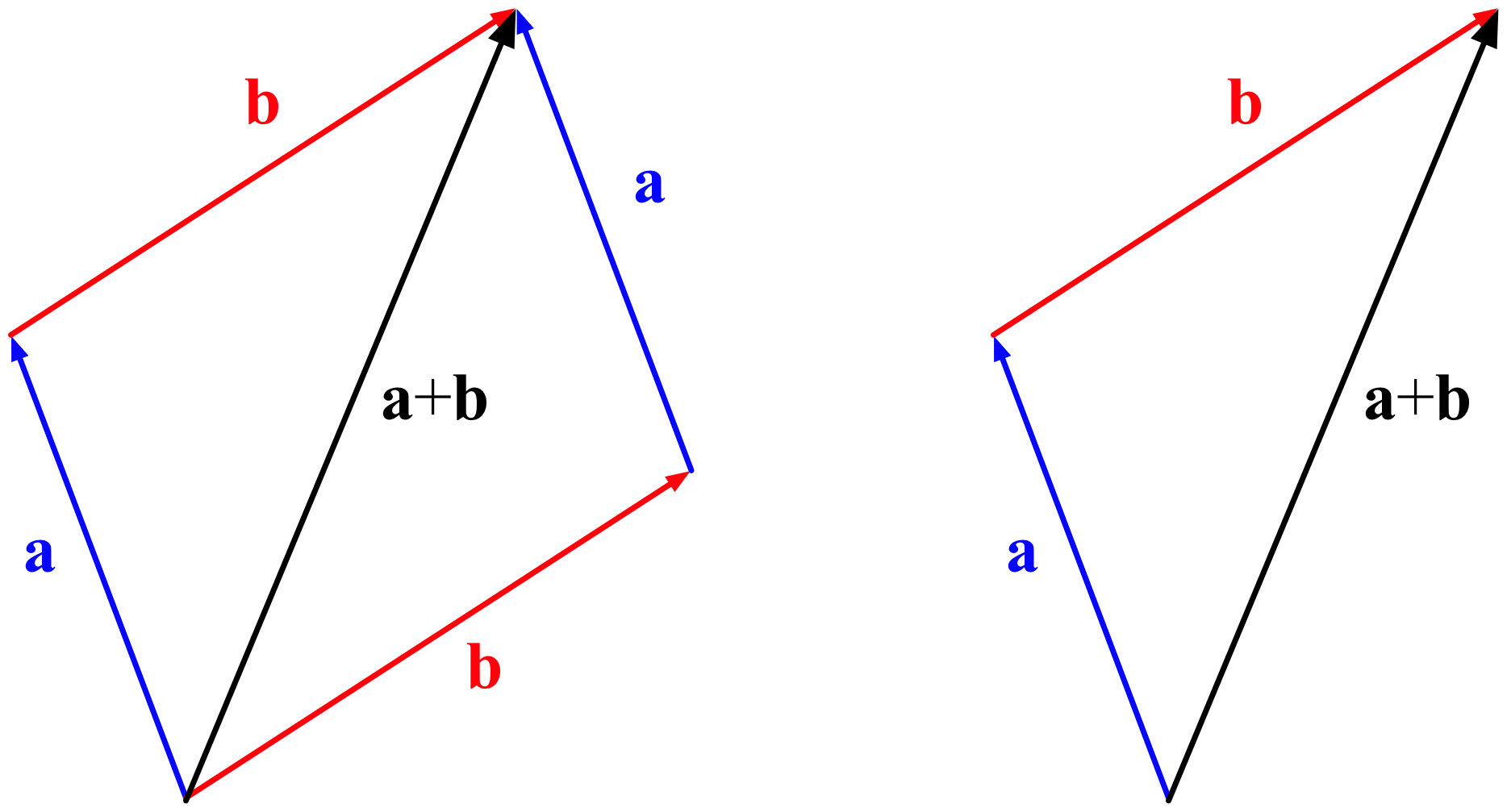
Now if there are two or more vectors that are required to be added, we use the Nose-tail method. Look at the definition above

Look at the example below:

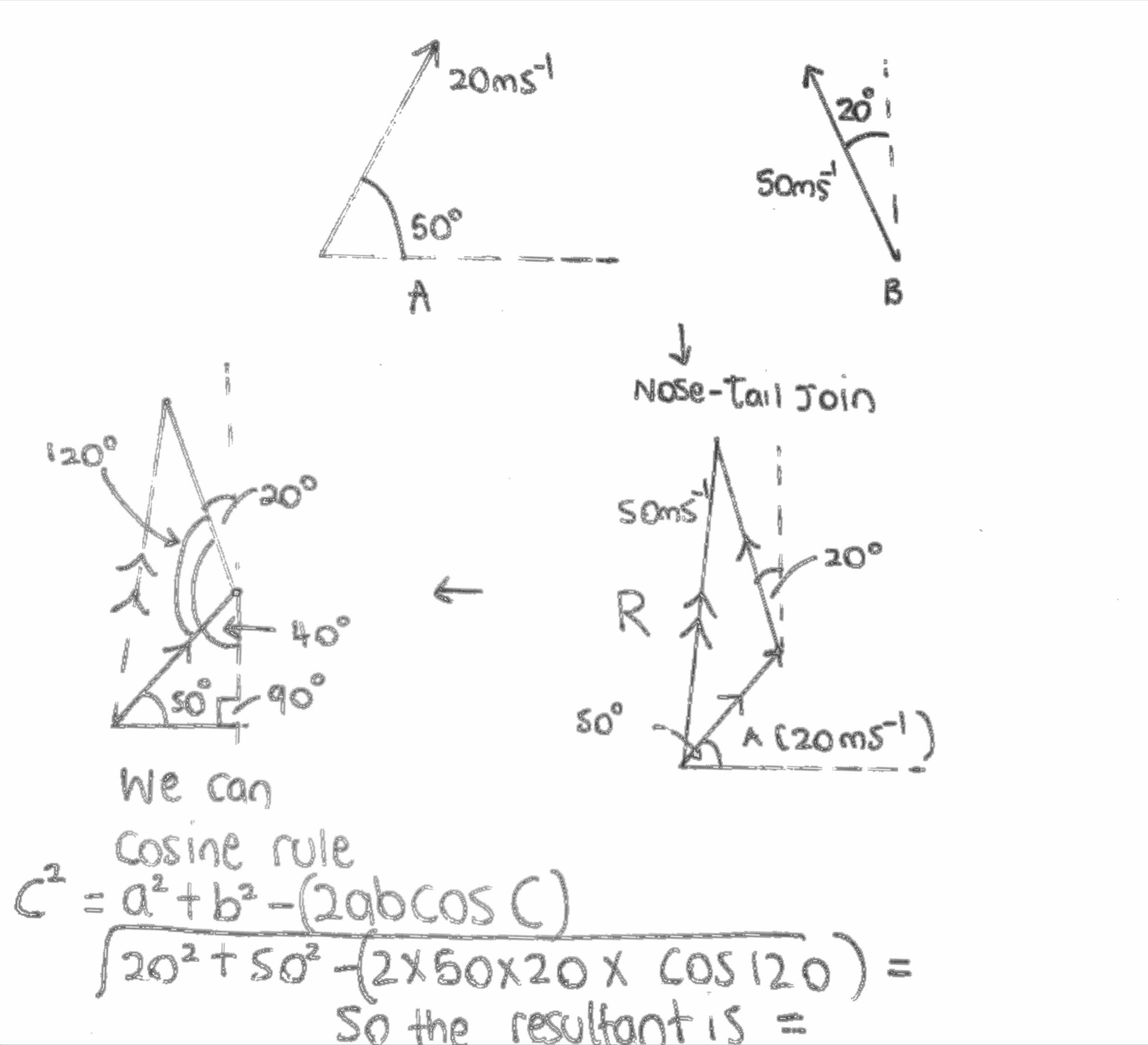
For example if a velocity is acting 20ms^-1 50° North from East

And a velocity is acting 50ms^-1 20° North from West

Both are acting on the same object at the same time.

We can solve it using trigonometry as shown above

However, as the resultant velocity is also a vector we must define the angle and so we use the sine rule

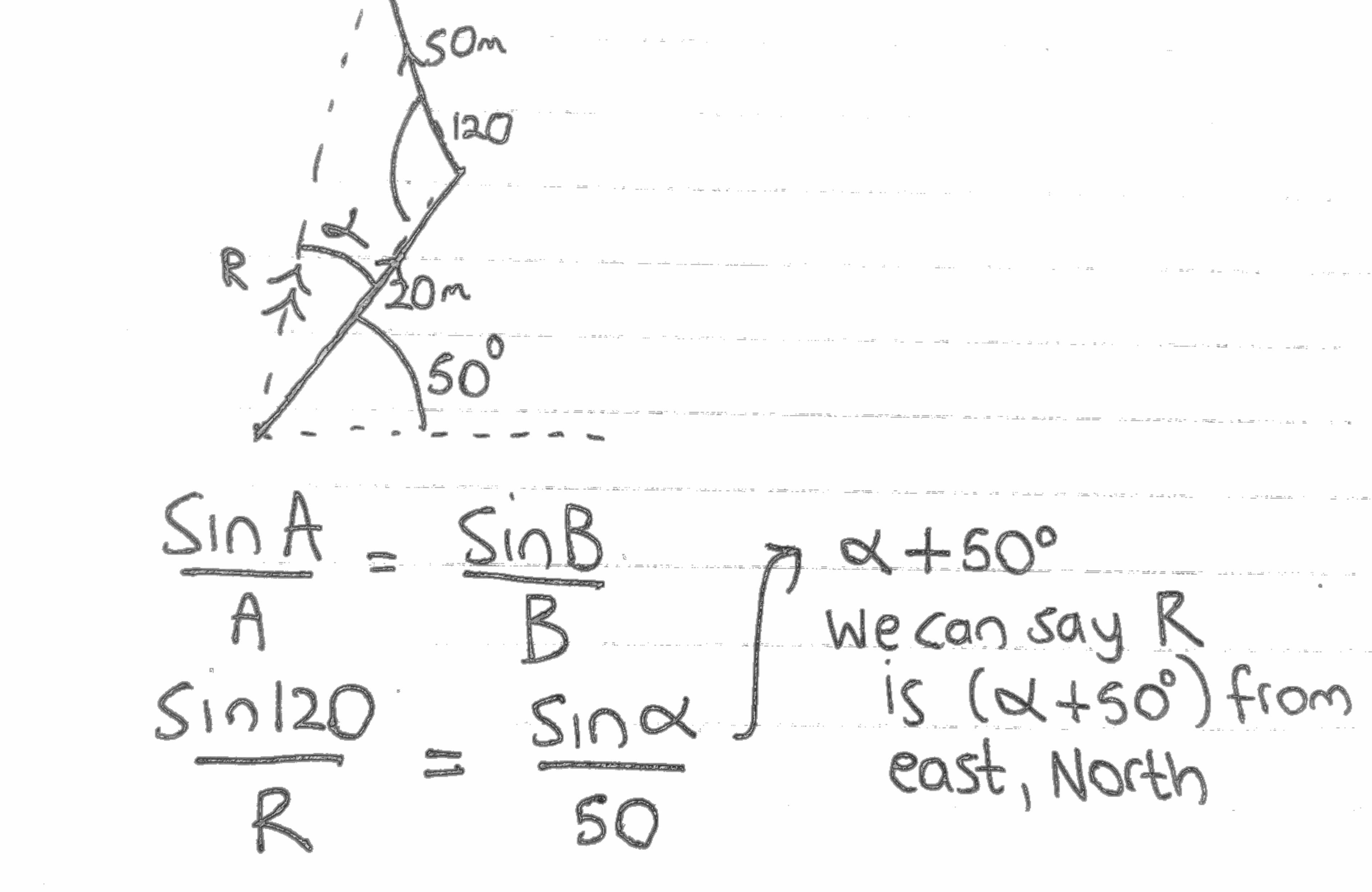
Resolving

Good to use this method always!

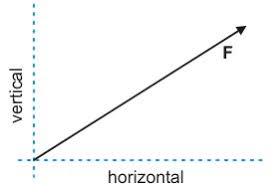
We Know that any vector can be split into two forces which are perpendicular to each other

For example:

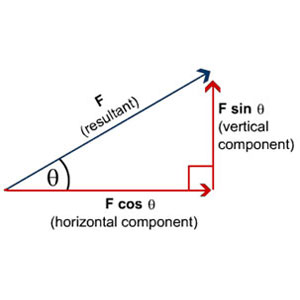
The horizontal component:

So Remember when the angle is CLOSED we get this:

Horizontal Component= FCosθ

The Vertical Component:

So when the angle is OPENED we get this:

Vertical Component = FSinθ

Do the same for the other Vectors

Then we only have up and down vectors. Nextly, we can add the vectors, if they are in the same direction. We can reduct/substract if they are in the opposite direction because, we can add or minus if vectors are in the same direction or in the opposite direction.

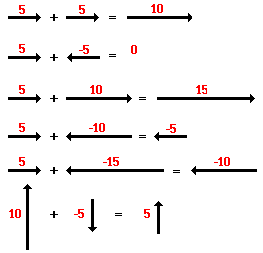
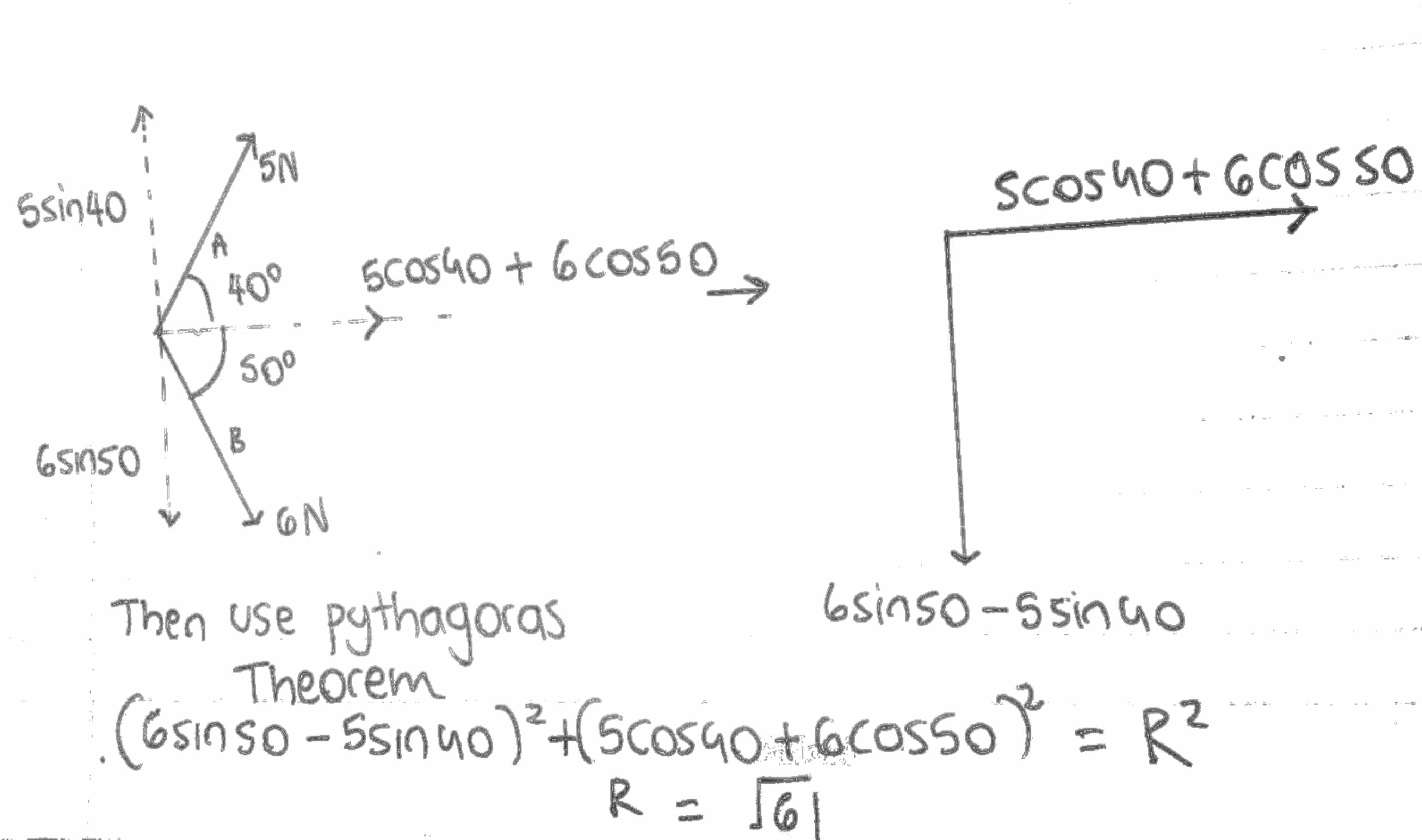
Finally, you will end up with the NET vertical vector and NET horizontal vector. Then use Pythagoras Theorem and find the resultant

Y² + X² = Resultant²

To get the direction take the Y and X and join them using the Nose-tail method and use we know that it is a right angle triangle so we can use Trigonometry

Look at the example below:

Adding 3 or more vectors

Use the same method(Nose-tail) and join the vectors end by end

Take one vector and add it to the back of another vector

Take the other vector and join the back of its end to the top of the other vector

Make sure the angles are noted and it is sketched properly. It must result in a longer chain or shape

Equilibrium

IMPORTANT POINTS

For anything to be in equilibrium There are two conditions:

• The NET resultant force must be equal to Zero

This is done by drawing/sketching



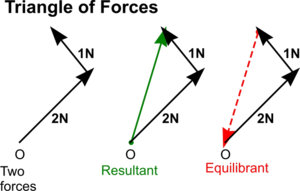
If the the vector diagram sketched is a triangle or closed like below - you have to say has the vector triangle is closed(Triangle of forces)/ the start of the vector ends at same point. So the resultant force is zero

In a different perspective, the resultant of the two vectors is cancelled out by the 3rd vector in order to have zero resultant.

• The Net Moment/Torque must be equal to zero

We will discuss about moment and torque later

They might ask many questions regarding this point.

So whenever they say an object is in equilibrium then the resultant force must be zero. So you need to keep in mind that the vector diagram must be a closed triangle.

You can either draw the vector triangle or diagram and it must be closed!

You also can solve by resolving - but this uses simultaneous equations and maybe the calculator. So use cos & sin instead.

When doing this method just remember the the vertical and horizontal component must be balanced(equilibrium).

Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...