Standing Waves, Fundamental Frequency & Harmonics

Stationary/Standing waves

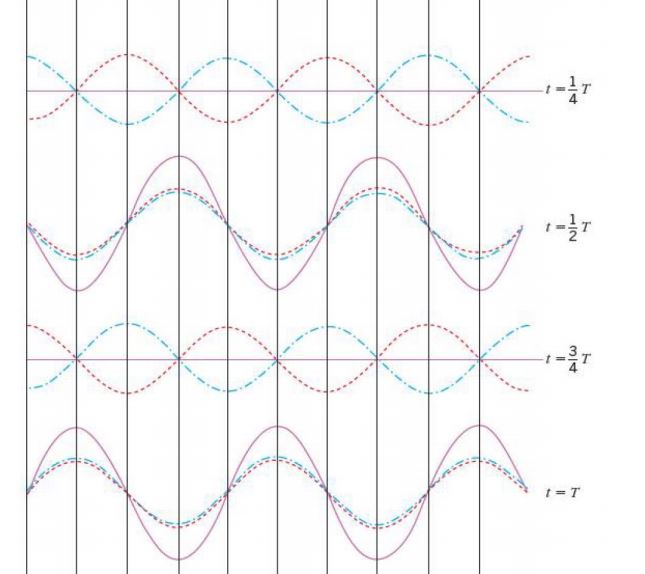
We can call it either a standing wave or a stationary wave but, we will use the term stationary wave

Stationary wave is formed when two progressive identical(same frequency and amplitude) waves move in the opposite direction and meet and superpose.

Think this of as when two trolley equal in mass and speed , collides with each other head to head. Probably, the result would be that there will be no speed and both are stationary.

However, as these are waves, the displacement is always changing and so at certain times and points, these waves superpose to form zero displacement(Out of phase) or maximum displacement(in phase).

The wave energy is said to be trapped at a particular point

So at one point, the two waves are out of phase and at every 1/4 of the period, the phase becomes in phase and out phase and so on

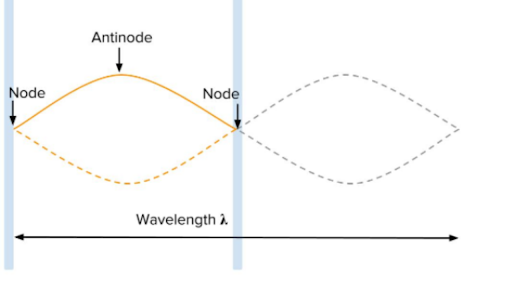
Antinodes and Nodes

In a stationary wave, each particle has its own unique amplitude. The word amplitude is used rather than the word displacement because, the maximum displacement for each particle remains constant and different for different particles. So each particle in a stationary wave has different accelerations

So the top part of the wave, particles are in phase. This is because, the particle all move up but, with different accelerations.

The top part and the bottom part of the waves are not in phase as half of the wave moves up and the other part moves down

There are 2 points in a stationary wave:

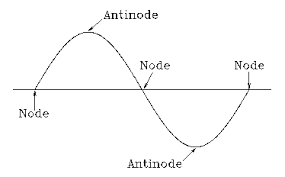
• Antinode

These are points in the wave which always have the highest amplitude



• Nodes

Points in a stationary wave which always has zero amplitude

You will need to know somethings of the wave

Wavelength

As we can see the length between two nearest antinodes or the length between two nearest node is actually half of the wavelength. Thus, the distance between two nodes or antinodes is half the wavelength(λ/2).

Thus, in finding the wavelength and finding also the frequency of this stationary wave, we can find the velocity of the wave!

v = fλ

But we know that the stationary waves has zero velocity and that they do not transfer energy.

This velocity is actually the velocity of the two identical progressive waves which were used to intially create the stationary wave

Now, we will see some Experiments used to find these wavelengths!

Experiments to find λ

There are many different experiments used to find the wavelength of a radio wave and sound waves but, we will only see one for each:

• Radio waves


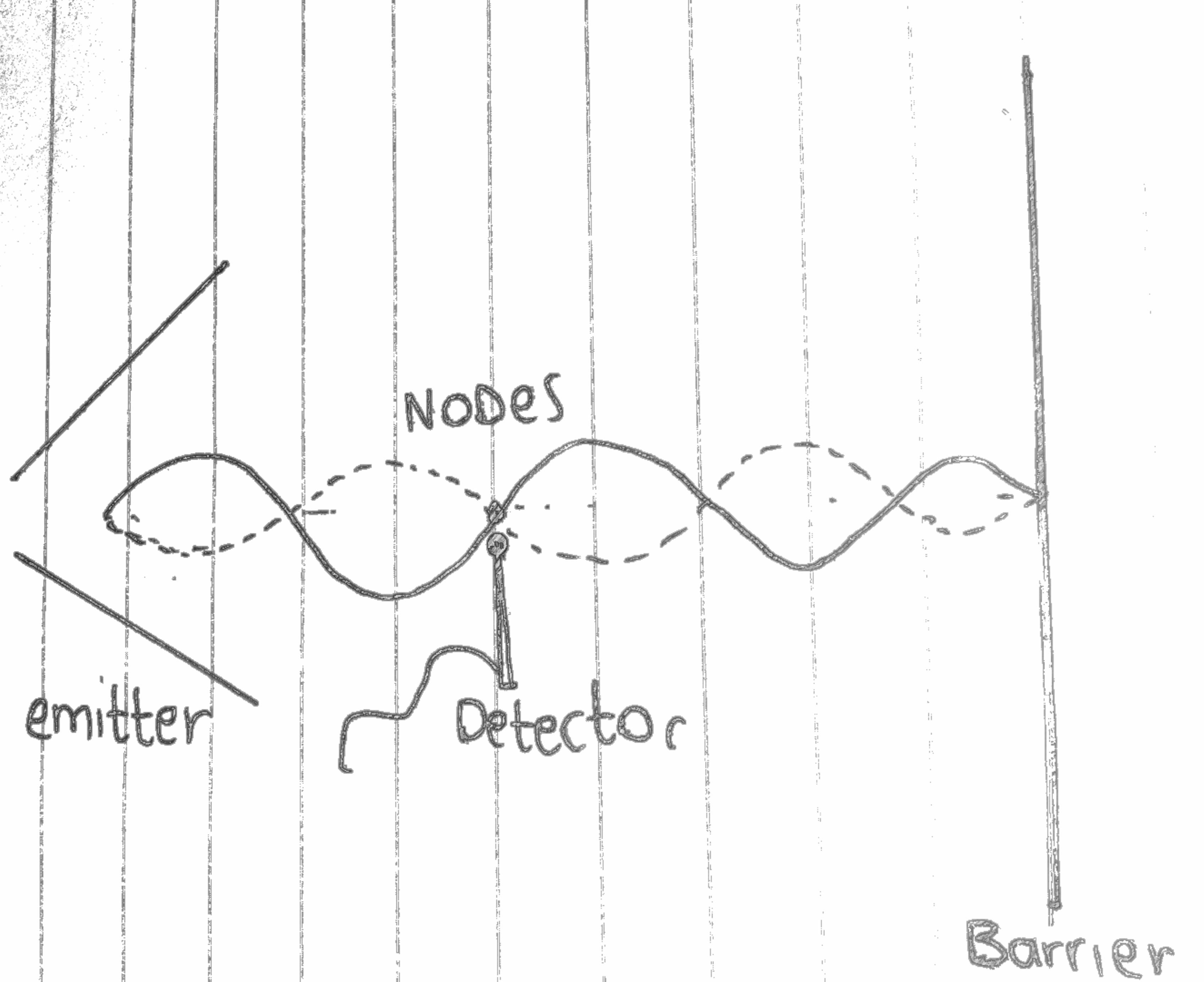
Usually an emitter is at one end and the reflector is placed at the other end

This will almost create a stationary wave, assuming no energy is lost.

A detector is moved from the emitters end to the reflector and the intensity or reading will change. It produce a series of maxima and minima readings.

The maximum readings are at the antinodes and the mimima readings are at the nodes

So we usually find the distance between 10 maxima (you also can take the distance between 10 minima if you want!). We do this to find the average distance between two nearest antinodes

Now this part gets a bit tricky. Most students always draw the wave of 10 antinodes

We can do this by using a simple formula I made

Distance between antinodes = Total Distance/(Number of Antinodes - 1)

d = T/(n-1)

We substract one because, this is the distance between 10 nodes so this literally means there are 9 Half waves between the two boundaries.

We know that the distance between two nearest Antinodes is half of the wavelength. To find the wavelength, we must multiply this distance by 2.

λ=2d

So after finding the wavelength we can use:

v= fλ

We can find the frequency of the wave because, radio waves have the same speed as light!

• Sound waves


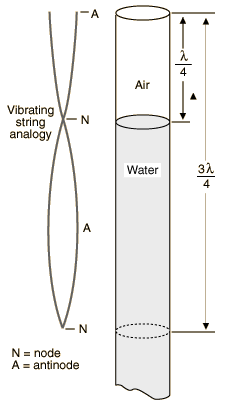
This also uses the same concept as above. However, we use different apparatus to measure the distance between many nodes or antinodes

For example:

A hollow tube open on both sides is immeresed in water so that the length of the pipe can be altered

So we usually use an emmiter which generates sound waves and so when a loud sound is made or heard, it is an antinode and a low sound is a node.

The same calcualtion is used but, this time the velocity is unknown whereas, the frequency of the sound wave source is known

Just to highlight. Many questions make it very simple by just saying the next loud sound is heard at this distance. So we just need to find the distance between this two Antinodes and this gives us half of wavelength

Fundamental frequency

In a string instrument or wind instrument, stationary waves are formed.

We will give a very concise summary for each instrument

But always remember this! At the barriers, it is always a node. This is actually very important to remember

Two ends or barriers

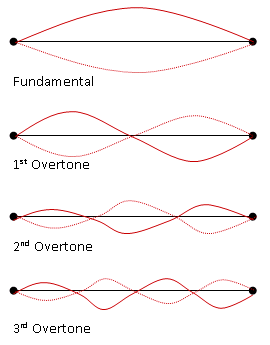
These are usually for guitars or string instruments and so at both ends must have a node.

So usually the first wave formed would be half a wave. The length of the string is L and so it equals to λ/2

L = λ/2

The wavelength of the wave is equal to twice the length of the string.

λ = 2L

When we apply:

v= fλ

v/λ= f

v/2L= f₀

When the wavelength takes the largest value or when the frequency is the smallest value, this is called the Fundamental frequency or the 1st harmonic

For the next possible frequency, the string must have two nodes at each end and also one in the middle

This gives us the wavelength of the wave

λ = L

v/λ= f

2*(v/2L)= f₁

The one for the fundamental frequency:

v/2L= f₀

So we substitute this into the new equation

2*f₀= f₁

Is same as:

v/L= f₁

The reason why we do that is to show that the next frequency formed is twice of the fundamental frequency and this is called the 2nd harmonic or the 1st overtone.

The pattern goes on and the next wave is 1.5λ. So we need to get 2L/3. The pattern goes on and the wavelength increases every time by half a wavelength. The next name is called 3rd harmonic or 2nd overtone and so on

One barrier and one open end

A good example is a bottle when you blow air into it

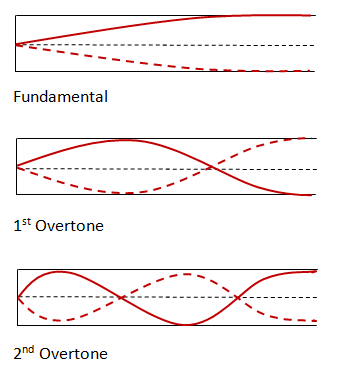
So always at the open end there is an Antinode and at the barrier, there is a node.

This is a bit tricker as we see the smallest wave formed is 1/4 of a wave.

As this is the distance between a node and an antinode ( not two antinodes or nodes)

λ = 4L

v/λ= f

v/4L= f₀

They have the same names so the lowest frequency formed is again called the fundamental frequency

The next possible frequency is when 3/4 of the wave is formed. Again the wavelength increases by 1/2 of a wave each time

3λ/4 = L

λ = 4L/3

v/4L/3 = f

3 * v/4L = f₁

This is same as:

3 * f₀ = f₁

This shows that the next wave formed is 3 times of the fundamental frequency and so this is different from a string instrument. This has the same name and is called the 1st over tone or the 2nd harmonic.

The next frequency formed is 5 times the fundamental frequency and so on

Both open ends

The same concept can be applied, so work it out

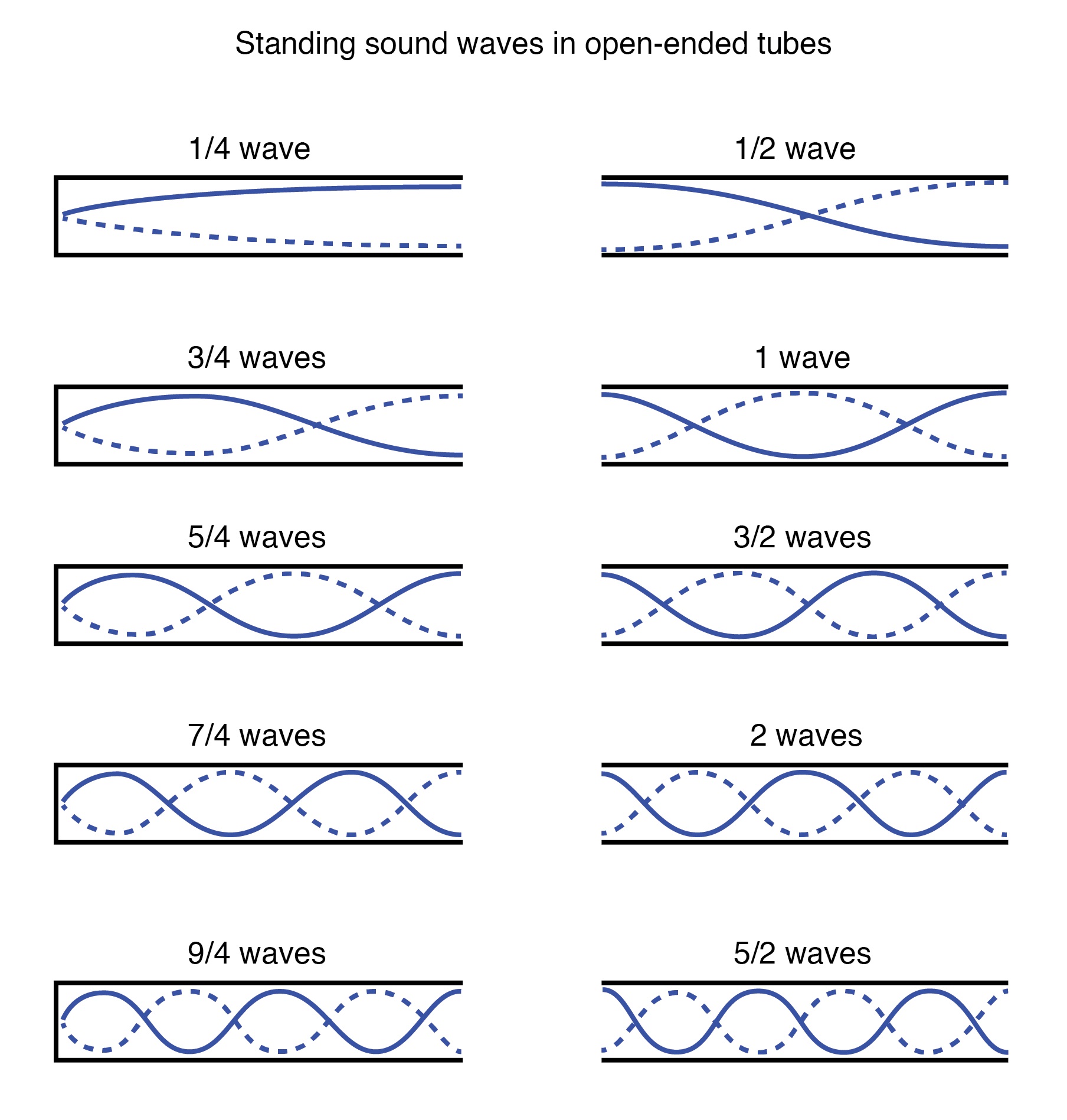
These principles of stationary waves formed are used in the above experiements!

Recommended

These are things you might like. Clicking these ads can help us improve our free services in the future...