Ideal Gases & Kinetic Theory Model

The state of matter depends on two factors:

The relative strength of attraction forces between particles

The stronger the relative strength between reactant particles the more closer the particles are and so it becomes a solid

The Kinetic energy of particles (Temperature)

The more kinetic energy, the particles posses, the faster they move away and take more space. So this makes the particles further apart amd thus makes the state more towards a gas when increased

These two factors have opposite effects on the state of matter and the final state of the matter depends on each of these factors. Usually more significant or prominent factor determines the state. For example, in a solid the relative strength between particles is more significant than the kinetic energy

An ideal and logical approach when comparing two substances at the same temperature is to compare the relative strengths between the particles (bonding or any IMF forces).

Ideal Gases

We will now talk specially about gases and in Chemistry, we come across a special type of gas known as the ideal gas. It is on the basis of the kinetic theory model. So let us consider the properties of an ideal gas / Assumptions of the kinetic theory model

Assumptions of the kinetic theory model

This is the same as the properties of an ideal gas. They are:

1. Gases are made from particles which are at constant motion

2. There are no attraction forces between particles in a gas

3. The particles have no volume/ the volume of particles are insignificant compared to the volume occupied by the gas

4. Collisions are perfectly elastic and so there is no loss in KE

5. Physics Knowledge - The Collision Time is insignificant compared to the time interval between collisions

These points gives us the description of an ideal gas. We can clearly see that no gas fits these descriptions but it can come close to it

When the bonding or attraction forces are super weak and the gas particles are small and particles are far apart, it best describes the Ideal gas

Good examples are Helium & Hydrogen gases and this almost follows the ideal gas trend

Also there are certain conditions which makes a real gas behave like a ideal gas:

1. High temperature - As particles will have more KE and the attraction forces between particles will be weak

2. Low pressure - Particles will be more spread out and occupy larger volumes (particle size does not increase)

The combined Law derivation

When we derive the famous law for ideal gases we need to know some other sub laws which are used to derive the combined law

Boyle's Law

The pressure is inversely proportional to the volume for a fixed mass and constant temperature

Pressure ∝ 1/Volume

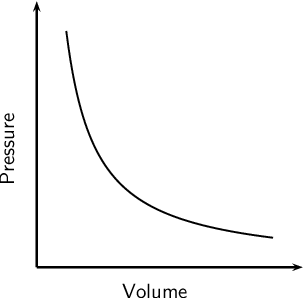
So remember this is Boyle's law and he states that PV = Constant

Charles' Law

The Volume is directly propotional to the Kelvin Temperature for a fixed pressure and mass

This could be used to derive that Pressure is directly proportional to the temperature for a fixed volume

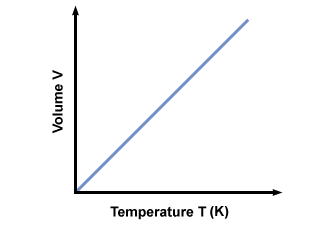
Pressure ∝ Temperature

Mole Law

There is no specific law for this but, it is quite obvious that when the number of moles increases the pressure increases

Pressure ∝ Moles

Combined Law

When we join all of these laws together we get this:

Pressure ∝ Temperature*Moles/Volume

Or:

Pressure * Volume ∝ Temperature*Moles

PV ∝ nT

To make this an equation we introduce a constant called the molar constant which has a specific value:

R = 8.314472

So the final combined law for ideal gases is:

PV = nRT

Points To Remember!

Always when using the combined law, make sure you use the correct units:

Volume : m³

Temperature : K

Pressure : Pa or Nm^-2

Only then we can use the value for molar constant as 8.314472

If we are using:

P₁V₁ = P₂V₂

It is not required to follow the SI units but the units must be consistent on both sides

What is Kelvin?

Kelvin is a unit used to measure temperature in the absolute scale

How we get Kelvin from Celsius:

Kelvin = °C + 273

More is not required...